Преобразование нестационарных временных рядов в стационарные
Реальные процессы свойством стационарности второго порядка могут и не обладать. Однако с помощью достаточно несложных преобразований часто удается привести наблюдаемый ряд к стационарному процессу. Примерами таких преобразований являются: а) взятие конечных разностей
б) логарифмирование цепных индексов
Применяется при экспоненциальном росте в) расчет темпов прироста
а также некоторые другие. При работе преобразование (30) более удобно, так как позволяет достаточно просто изменять временные серии исходных данных в связи, например, с укрупнением временных интервалов. Пусть возникла необходимость проанализировать временные ряды серии удвоенного временного интервала (t –1, t +1), т.е., например, Для такой серии преобразование (30) приводит к следующему временному ряду:
где Его величина представляет собой простую арифметическую сумму преобразованных значений показателей исходных интервалов, объединение которых привело к новой серии. В то же время для преобразования (31) в этом случае получим более сложное выражение, определяющее для значения нового временного ряда:
Для превращения исходного нестационарного ряда в стационарный могут быть использованы и другие преобразования. Например, В условиях постоянства математического ожидания и дисперсии особенности конкретного стационарного процесса второго порядка полностью определяются характером его автокорреляционной функции, имеющей вид зависимости значений коэффициентов автокорреляции от сдвига. Иными словами, автокорреляционная функция является дискретной и представляет собой последовательность значений коэффициентов автокорреляции Аналогично можно сформировать автоковариационную функцию стационарного процесса Все множество стационарных процессов второго порядка в общем случае в зависимости от особенностей их автокорреляционных функций разбивается на несколько однородных групп, для каждой из которых можно подобрать и построить адекватную модель. В общем случае можно выделить три группы таких моделей – модели авторегрессии, модели скользящего среднего и смешанные модели авторегрессии-скользящего среднего.
|

 . (28)
. (28) – первая разность. Это преобразование целесообразно использовать, когда закон изменения
– первая разность. Это преобразование целесообразно использовать, когда закон изменения 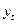 близок к линейному.
близок к линейному. . (29)
. (29)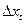 – вторая разность. Преобразование применяется, когда закон изменения
– вторая разность. Преобразование применяется, когда закон изменения  . (30)
. (30)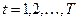 ;
; , (31)
, (31)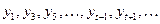 .
.
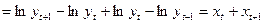 , (32)
, (32)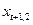 – преобразованное значение показателя на удвоенном интервале.
– преобразованное значение показателя на удвоенном интервале.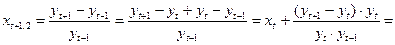
 . (33)
. (33) ,
,  и т.д. В каждом конкретном случае, выбирая преобразование, необходимо исходить из примерной формы временного графика зависимости
и т.д. В каждом конкретном случае, выбирая преобразование, необходимо исходить из примерной формы временного графика зависимости  .
. , поставленных в зависимость от сдвига i, где
, поставленных в зависимость от сдвига i, где  .
. поставленных в зависимость от сдвига i. Напомним, что между соответствующими значениями этих функций существует однозначная взаимосвязь
поставленных в зависимость от сдвига i. Напомним, что между соответствующими значениями этих функций существует однозначная взаимосвязь  , т.е.
, т.е.  .
.


