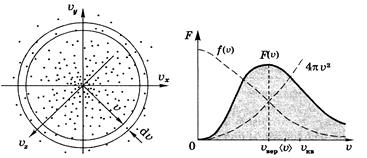
Распределение молекул по модулю скорости
Найдем вероятность или относительное число молекул, модуль скорости которых заключен в интервале (v, v + dv) (рисунок). Объем этого слоя равен произведению поверхности слоя на его толщину, т.е. 4 pv 2 dv, объемная же плотность вероятности f (v) во всех точках слоя одинакова. Следовательно, вероятность попадания в этот слой dP = f (v) 4 pv 2 dv
Величина dP / dv - мы ее обозначим F (v) - характеризует искомую вероятность, т.е. F (v) = 4 pv 2 f (v):
Эта формула представляет собой закон распределения Максвелла по модулю скорости. Вид функции F (v) показан на рисунке. Эта функция тоже нормирована на единицу:
На рисунке пунктиром представлена «конструкция» (сомножители) функции F (v). Заметим, что в отличие от F (v) площадь под кривой f (v) физического смысла не имеет (физический смысл имеет интеграл по объему от f (v)). Распределения Максвелла не зависит ни от структуры молекул, ни от того, как они взаимодействуют друг с другом. Поэтому они применимы не только к газам, но и к другим агрегатным состояниям вещества.
Характерные скорости
К ним относятся три скорости: наиболее вероятная v вер, средняя á v ñ и среднеквадратичная v кв. Наиболее вероятной скорости соответствует максимум функции распределения F (v). Эта скорость определяется из условия dF / dv = 0, откуда следует v вер =
|