Очевидно, что у перпендикулярных прямых направляющие и нормальные вектора должны быть ортогональны, и следовательно, скалярные произведения векторов должны быть равны нулю.
 . (4.15)
. (4.15)
Угловые коэффициенты перпендикулярных прямых должны быть обратны по величине и противоположны по знаку.
 . (4.16)
. (4.16)
 . (4.17)
. (4.17)
Пример4.. Найти уравнение прямой, проходящей через точку М 0(1;-2) перпендикулярно прямой, проходящей через точки М 1(3;2) и М 2(-1;1).
Найдем уравнение прямой, проходящей через точки М 1 и М 2, используя формулу (4.7).
 . Направляющий вектор этой прямой
. Направляющий вектор этой прямой  будет коллинеарен нормальному вектору искомой прямой
будет коллинеарен нормальному вектору искомой прямой  ,т.е.
,т.е.
 . Можно взять нормальный вектор
. Можно взять нормальный вектор  .Тогда искомое уравнение принимает вид
.Тогда искомое уравнение принимает вид 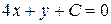 .Поскольку точка М 0(1;-2) принадлежит этой прямой, её координаты должны удовлетворять уравнению. 4*1+1*(-2)+ С =0 → С =-2. Окончательно уравнение искомой прямой имеет вид
.Поскольку точка М 0(1;-2) принадлежит этой прямой, её координаты должны удовлетворять уравнению. 4*1+1*(-2)+ С =0 → С =-2. Окончательно уравнение искомой прямой имеет вид  .
.
Расстояние от точки до прямой
Пусть прямая l задана общим уравнением  . Требуется найти расстояние до неё от точки
. Требуется найти расстояние до неё от точки  .
.
 Возьмем текущую точку прямой
Возьмем текущую точку прямой  . Расстояние от точки до прямой будет равно модулю проекции вектора
. Расстояние от точки до прямой будет равно модулю проекции вектора  на нормальный вектор прямой
на нормальный вектор прямой  . (См. рис 4.2).
. (См. рис 4.2).
 . Преобразуем получившееся равенство добавив и вычтя в числителе С.
. Преобразуем получившееся равенство добавив и вычтя в числителе С.
 . Поскольку точка
. Поскольку точка  - текущая точка прямой, выражение
- текущая точка прямой, выражение  . Окончательно
. Окончательно  . (4.18).
. (4.18).
Линии второго порядка на плоскости.

 . (4.15)
. (4.15) . (4.16)
. (4.16) . (4.17)
. (4.17) . Направляющий вектор этой прямой
. Направляющий вектор этой прямой  будет коллинеарен нормальному вектору искомой прямой
будет коллинеарен нормальному вектору искомой прямой  ,т.е.
,т.е. . Можно взять нормальный вектор
. Можно взять нормальный вектор  .Тогда искомое уравнение принимает вид
.Тогда искомое уравнение принимает вид 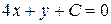 .Поскольку точка М 0(1;-2) принадлежит этой прямой, её координаты должны удовлетворять уравнению. 4*1+1*(-2)+ С =0 → С =-2. Окончательно уравнение искомой прямой имеет вид
.Поскольку точка М 0(1;-2) принадлежит этой прямой, её координаты должны удовлетворять уравнению. 4*1+1*(-2)+ С =0 → С =-2. Окончательно уравнение искомой прямой имеет вид  .
. .
. Возьмем текущую точку прямой
Возьмем текущую точку прямой  . Расстояние от точки до прямой будет равно модулю проекции вектора
. Расстояние от точки до прямой будет равно модулю проекции вектора  на нормальный вектор прямой
на нормальный вектор прямой  . (См. рис 4.2).
. (См. рис 4.2). . Преобразуем получившееся равенство добавив и вычтя в числителе С.
. Преобразуем получившееся равенство добавив и вычтя в числителе С. . Поскольку точка
. Поскольку точка  . (4.18).
. (4.18).


