Параметрические уравнения линий на плоскости.

Параметрические уравнения линии на плоскости в декартовой системе координат представляют собой систему двух уравнений

(3.1)

Параметрические уравнения задают линию как траекторию движения точки во времени.

Пример 2. Найти уравнение окружности радиусом R с центром в начале координат в параметрической форме.

Из рис.3.1 очевидно следует система параметрических уравнеий

(3.2)

 

Уравнения прямой на плоскости.

 

Уравнение прямой с угловым коэффициентом

Пусть на плоскости Oxy задана прямая, не параллельная оси Oy и пересекающая её в точке N (0;b), образующая угол α; с положительным направлением оси 0x (0≤α<π).

Рис.4.1.в

Рис.4.1.в

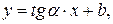Возьмем текущую точку прямой . Из рисунка 4.1.а видно, что обозначим . В этом случае уравнение прямой примет вид

(4.1), где

k – тангенс угла наклона прямой к оси Ox, b – ордината точки пересечения прямой и оси Oy.

Рассмотрим частные случаи уравнения прямой с угловым коэффициентом.

Пусть прямая проходит через начало координат. Тогда и уравнение (4.1) принимает вид (4.2). (См. рис. 4.1.б)

Пусть прямая параллельна оси Ox, тогда tg α= tg 0=0 и уравнение прямой принимает вид

(4.3) (См. рис. 4.1.в).

Пусть прямая параллельна оси Oy. В этом случае уравнение (4.1) теряет смысл, т.к. а не определен. У прямой параллельной оси Oy постоянное значение абсцисс, т.е.

(4.4) (См. рис. 4.1.г).

Заметим, что а – абсцисса точки пересечения прямой с осью Ox.