Окружность - простейшая линия второго порядка. Её уравнение было получено ранее как линии, все точки которой равно отстоят от центра.
 (5.1)
(5.1)
Это уравнение называется каноническим уравнением окружности.
 - координаты центра окружности, r радиус окружности.
- координаты центра окружности, r радиус окружности.
5.2. Эллипс
 Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, величина постоянная. Пусть точки
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, величина постоянная. Пусть точки 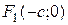 и
и  - фокусы эллипса и расстояние между ними равно 2 с. Сумма расстояний от любой точки эллипса обозначим 2 а. 2 а>;2 с → а> с. (См. рис. 5.1.а).
- фокусы эллипса и расстояние между ними равно 2 с. Сумма расстояний от любой точки эллипса обозначим 2 а. 2 а>;2 с → а> с. (См. рис. 5.1.а).
Пусть фокусы (точки 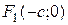 и
и  лежат на оси 0 x, а начало координат находится посередине отрезка
лежат на оси 0 x, а начало координат находится посередине отрезка  . и пусть точка
. и пусть точка  - текущая точка эллипса.
- текущая точка эллипса.
 , т.е.
, т.е.  .
.
Приведем полученное уравнение эллипса к канонической форме.
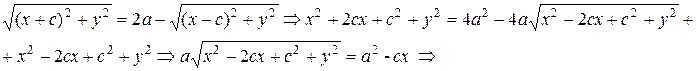
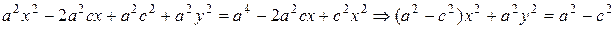 .
.
Положим  . Тогда уравнение принимает вид
. Тогда уравнение принимает вид  . Разделив обе части уравнения на
. Разделив обе части уравнения на 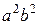 , получим каноническое уравнение эллипса
, получим каноническое уравнение эллипса
 (5.2)
(5.2)
Установим форму эллипса исходя из его канонического уравнения.
Поскольку обе переменные входят в четной степени, кривая симметрична относительно координатных осей и начала координат. Найдем точки пересечения эллипса с координатными осями.
Пусть  . Таким образом, точки
. Таким образом, точки  и
и  - точки пересечения с осью 0x. Положив x =0. аналогичными операциями получаем точки пересечения эллипса с осью 0y
- точки пересечения с осью 0x. Положив x =0. аналогичными операциями получаем точки пересечения эллипса с осью 0y  и
и  . Найденные точки называются вершинами эллипса, а отрезки
. Найденные точки называются вершинами эллипса, а отрезки  , а также их длины 2 a и 2 b, называются большой и малой осью эллипса. Числа a и b называются большой и малой полуосями. Из уравнения (5.2) следует, что каждое из слагаемых не превосходит единицы.
, а также их длины 2 a и 2 b, называются большой и малой осью эллипса. Числа a и b называются большой и малой полуосями. Из уравнения (5.2) следует, что каждое из слагаемых не превосходит единицы.  , т.е. все точки эллипса лежат внутри прямоугольника со сторонами
, т.е. все точки эллипса лежат внутри прямоугольника со сторонами  Из уравнения (5.2) следует,что увеличение одной переменной ведет к уменьшению другой. Таким образам эллипс имеет форму, изображенную на рис.5.1.б.
Из уравнения (5.2) следует,что увеличение одной переменной ведет к уменьшению другой. Таким образам эллипс имеет форму, изображенную на рис.5.1.б.
В качестве характеристики формы эллипса используется  эксцентриситет эллипса.
эксцентриситет эллипса.
При b=a эксцентриситет равен 0, а сам эллипс превращается в окружность.  . Чем ближе значение эксцентриситета к 1, тем эллипс оказывается более сплющенным.
. Чем ближе значение эксцентриситета к 1, тем эллипс оказывается более сплющенным.
ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ

 (5.1)
(5.1) - координаты центра окружности, r радиус окружности.
- координаты центра окружности, r радиус окружности. Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, величина постоянная. Пусть точки
Эллипсом называется множество точек плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, величина постоянная. Пусть точки 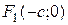 и
и  - фокусы эллипса и расстояние между ними равно 2 с. Сумма расстояний от любой точки эллипса обозначим 2 а. 2 а>;2 с → а> с. (См. рис. 5.1.а).
- фокусы эллипса и расстояние между ними равно 2 с. Сумма расстояний от любой точки эллипса обозначим 2 а. 2 а>;2 с → а> с. (См. рис. 5.1.а). . и пусть точка
. и пусть точка  - текущая точка эллипса.
- текущая точка эллипса. , т.е.
, т.е.  .
.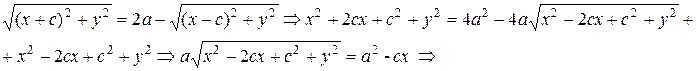
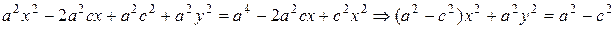 .
. . Тогда уравнение принимает вид
. Тогда уравнение принимает вид  . Разделив обе части уравнения на
. Разделив обе части уравнения на 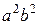 , получим каноническое уравнение эллипса
, получим каноническое уравнение эллипса (5.2)
(5.2) . Таким образом, точки
. Таким образом, точки  и
и  - точки пересечения с осью 0x. Положив x =0. аналогичными операциями получаем точки пересечения эллипса с осью 0y
- точки пересечения с осью 0x. Положив x =0. аналогичными операциями получаем точки пересечения эллипса с осью 0y  и
и  . Найденные точки называются вершинами эллипса, а отрезки
. Найденные точки называются вершинами эллипса, а отрезки  , а также их длины 2 a и 2 b, называются большой и малой осью эллипса. Числа a и b называются большой и малой полуосями. Из уравнения (5.2) следует, что каждое из слагаемых не превосходит единицы.
, а также их длины 2 a и 2 b, называются большой и малой осью эллипса. Числа a и b называются большой и малой полуосями. Из уравнения (5.2) следует, что каждое из слагаемых не превосходит единицы.  , т.е. все точки эллипса лежат внутри прямоугольника со сторонами
, т.е. все точки эллипса лежат внутри прямоугольника со сторонами  Из уравнения (5.2) следует,что увеличение одной переменной ведет к уменьшению другой. Таким образам эллипс имеет форму, изображенную на рис.5.1.б.
Из уравнения (5.2) следует,что увеличение одной переменной ведет к уменьшению другой. Таким образам эллипс имеет форму, изображенную на рис.5.1.б. эксцентриситет эллипса.
эксцентриситет эллипса. . Чем ближе значение эксцентриситета к 1, тем эллипс оказывается более сплющенным.
. Чем ближе значение эксцентриситета к 1, тем эллипс оказывается более сплющенным.


