шпонок.
4.1. Расчет входного вала.
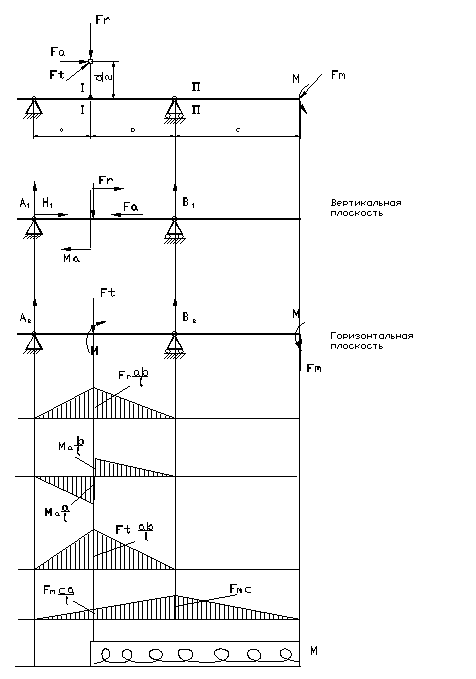
4.1.1. Определение диаметров под шестерню, подшипник и муфту вала. Крутящий момент, Нмм Мкр1 = 44,8 Нм. Окружная сила Ft1= 2Mкр1/dm1= 2*44,8*103/46=1948 H. Радиальная сила Fr1= Ft1 tga cosd1 =1948*0,364*0,97= 687,8 Н, Осевая сила Fa1= Ft1 tga*sind1 = 172 Н. Радиальное усилие на муфте Fm1= 250(Мкр1)1/2 = 1673 Н. Принимаем материал вала - сталь 45 улучшенная с пределом прочности sв = 750 МПа, пределом текучести sт = 450 МПа. Принимаем также допускаемое напряжение на кручение [t] = 12 МПа. Тогда предварительный диаметр вала d= {Мкр1/(0,2[t])}1/3 = {44,8*103/(0,2*12)}1/3 = 26,52 мм. Выбираем: Посадка шестерни на диаметр, мм dш1=30 мм, ширина шестерни,мм bw = 31,6 мм Диаметр в месте посадки подшипников dп1= 35 мм; месте посадки муфты dм1= 30мм. 4.1.2. Выбор подшипников и определение схемы размещения опор. Предварительно выбираем подшипники и по ним оцениваем конструкцию вала- шестерни с осевыми размерами. Схема размещения опор приведена на рис. П2. 3. Используя принцип подобия, примем следующие плечи вала: a1= 25 мм; b1= 45 мм; c1= 40 мм; l1= a1+ b1=\25+ 45= 70 мм.
Рис. П2.3
4.1.3. Расчет реакций опор. Определим допускаемую радиальную нагрузку на входном валу при Ft1 = 1948 Н. Определим реакции в опорах: в вертикальной плоскости изгибающий момент Ма= 0,5Fa1dm1 = 3956 Нмм. А1 = (Fr1 (a1 + b1)- Ма) / b1 = [687,8*(25+45)- 3956]/45= 982 H. В1 = [Ма - Fr1 a1]/b1 = 294,2 H. (Знак минус будет означать, что реакция опоры В1 направлена вниз.) В горизонтальной плоскости А2 = [Ft (a1 + b1)- Fm1 *c1 ]/b1 = [1948*70- 1673*40]/45= 1543,1 H. В2 = (Ft1+ Fm1) – A2 = (1948+ 1673)- 1543,1= 2077,9 H. Суммарная реакция в опорах, Н А = (А12 + А22)1/2 = (9822+ 1543,12)1/2= 1829 H. В = (В12 + В22)1/2 = (294,2 2+ 2077,9 2)1/2= 2098,6 H. Наиболее нагружена опора B. 4.1.4. Определение напряжений и запасов прочности. Для сечения I изгибающий момент равен М1= {(Fк1 a1)2+ (Ft a1)2+ (Ma)2}1/2= 51,8*103 Нмм Напряжение изгиба определим по формуле 15.5 [4], МПа: sи= М1/(0,1*dп 3)= 51,8*103 /(0,1*353)= 12,08 МПа Напряжения кручения t = Мкр1/(0,2* dп3)= 44,8*103/(0,2* 353)= 5,2 МПа. s-1= 0,4 sв = 0,4*750= 300МПА. t-1= 0,2sв = 150 МПа, tв= 0,6sв= 450 МПа. По рекомендациям [4] принимаем sа=sи; ta=tm= 0,5t.; ys= 0; yt= 0,05. По табл. 15.1 для галтели Кs = 1,85; Кt=1,4 По графику (рис.15.5 кривая2) Kd=0,72. По графику (рис. 15.6) для шлифованного вала КF= 1. Находим запас сопротивления усталости по изгибу Ss=s-1/[saKs/(KdKF)+yssm] = 300*0,72/(12,08*1,85)= 9,66. St= t-1/[taKt/(KdKF)+ yttm]= 150/[2,6*1,4/(0,72*1)+ 0,05*2,6)]= 28,9 Откуда при совместном действии сил S= Ss* St/(S2t+ S2s)1/2 = 9,16 >1,5.
Для второго сечения изгибающий момент равен Ми2@ -Fm1 c1 = -1673*40= = -66,9*103 Нмм Напряжения изгиба sи2= Ми2/(0,1*dв 3) = 66,9*103/(0,1* 353)= 15,6 МПа; кручения t2= Мкр1/(0,2* dп 3) = 44,8*103/(0,2* 353)= 5,2 МПа. Принимаем радиус галтели, равным 2 мм. По табл. 15.1[4] находим Ks= 1,85; Kt= 1,6 Определяем запасы сопротивления усталости по изгибу Ss= s-1/[saKs/(KdKF)+ yssm] = 300*0,72/(15,6*1,85)= 7,48; по кручению St= t-1/[taKt/(KdKF)+ yttm] = 150/[2,6*1,4/(0,72*1)+ 0,05*2,6)]= 28,9. S= Ss* St/(S2t+ S2s)1/2 = 7,24. Больше напряжено 2-е сечение Проверяем статическую прочность при перегрузках, когда напряжения удваиваются, МПа sэк= (s2и2+ 3t2 2)1/2= [(2*15,6)2+ 3*(2*5,2)2]0,5= 36,02 МПа. Должно быть меньше [s]@ 0,8sт= 0,8* 450= 360 МПа. 4.1.5. Проверка жесткости вала. Наиболее опасным здесь является перемещение шестерни. Для определения прогиба вычислим момент инерции сечения вала, мм4 J= pd4п/64= p 354/64= 7,36*104. Прогиб в вертикальной плоскости равняется от силы Fr1, мм yв1 = Fr1a1 2(b1 +a1)/(3EJ) = 687,8*252(25+45)/(3* 2,1*105*7,36*104)=6,48*10-4мм; от момента Ма прогиб равен yв2 = Maa21/(2EJ)= 3956*252/(2*2,1*105*7,36*104)= 0,8*10-4мм, т.е. yв = yв1 - yв2 = (6,48- 048)10-4 = 5,68*10-4мм. Прогиб в горизонтальной плоскости от силы Ft равен yг= Ft1 а1 2(b1 +a1)/(3EJ) = 1948*252(25+45)/(3* 2,1*105*7,36*104)= 1,84*10-3мм Суммарный прогиб равен, мм Y= (y2в+ y2г)1/2 = 10-4 (5,682 +18,42)1/2 = 1,92*10-3мм. Допускаемый прогиб [y]@ 0,01*m= 0,01*2= 0,02 мм. 4.1.6. Определение резонансных частот. Масса шестерни, mш = 7,8*10-6*0,786* d2m1bw cos( 14°2’10” ) = 7,8*10-6* 0,786*462 33,6*0,97 = = 0,423кг. Резонансные частоты круговая wr1= {3ЕJ/[mc12(l1 +c1)]}1/2 = {3*2,1*105*7,36*104/ [0,423*402*110]}1/2 = = 7,89*102 рад/сек; периодическая nr= wr1/(2p)= 1,26*102Гц. Первая критическая частота вращения, при которой возможен резонанс, равна nкр1= 60n1r= 7560 об/мин. Вторая критическая частота вращения от зубцовых колебаний nкр2= 60 n1r / z1= 60 * 7560/23= 19,7*103 об/мин. Крутильная упругость вала, 1/(Нмм)= 10-3(с2кг-1мм-2) Jк= 2*(b1 +c1)/[8*105(dсв1/2)4] = 2*(45+40)/[8*105*103 (31,69/2)4]= 3,37*10-9, где dсв1@ [(dм1+ c1) dм1 2+ b1dn2+ adш12)/(dм1+ b1 + c1+ a1)]1/2= (140625 /140)1/2=31,69мм- средний диаметр вала. Маховой момент шестерни, кгмм2 Jмах= mшR2/2 = mш (dm1/2)2/2 = 0,423 (46/2)2/2= 111,88 Крутильные резонансные частоты круговая wkr= (JмахJк)-1/2 = 0,163*104 рад/сек; периодическая nkr= wkr/(2p)= 259,3 Гц Третья критическая частота вращения вала, об/мин nкр3= wk2*60/(2p) = 2477. Четвертая критическая частота вращения от зубцовых колебаний nк42= 60 nkr / z1= 60 * 259,3/23= 676,4 об/мин. Критические частоты вращения не совпадают с частотой вращения входного вала. 4.1.7. Проверочный расчет подшипников качения на входном валу. Ресурс подшипников Lh0= 24000 час. Исходя из диаметральных размеров выбираем роликовые конические однорядные подшипники серии 20007307, имеющие Са= 59780 H; С0= 45080 H. Находим Fa1/C0=0,004 Суммарные радиальные составляющие, Н Fr1= (A21+ A22)1/2 = 1829 H Fr2= (B21+ B22)1/2 = 2048,6 H. По табл. 16.5 [4] находим e= 1,5*ctg a. Из каталога следует a»12° и e=7,1 и далее при V=1 Fa1/(VFr max)= 172/2048,6= 0,084 При этом X=1, Y=0. По рекомендациям [4] принимаем Кs= 1,3; Кт = 1. Тогда радиальная нагрузка Pr= Fr max*1,3= 2048,6,4*1,3= 2663,2 H. Используя графики типовых режимов (рис. 8.42 [1]), эквивалентную долговечность определим, час LhE= KHELh0= 0,25*240000= 6000. Находим эквивалентный ресурс LE = 60*10-6*n*LhE=60 *10-6*960*6000= 345,6млн. обор. При а1=1, а2=1, р=3,33 определим динамическую грузоподъемность, Н C= Pr [LE /(a1a2)]1/P = 2663,2(345,6)1/3,33= 15407,7 H. Это меньше паспортной динамической грузоподъемности. Проверяем подшипник по статической грузоподъемности c учетом 2-х кратной перегрузки. P0= X0Fr max+ Y0Fa = 2(0,6 Frmax+0,5Fa1)= 2(0,6*2048,6+ 0,5*172)= 2630,3H. Сравниваем с данными каталога. Если они меньше или существенно больше, то следует выбрать другой подшипник. Таким образом, выбираем подшипник серии 20007107. Са= 25088 Н; С0= 22540 Н.
4.1.8. Выбор и расчет шпонок Шестерня. Из справочника [5] для диаметра 30 мм выбираем призматическую шпонку 8х7х30 ГОСТ 23360- 78 из чистотянутой стали с пределом прочности свыше 600 МПа. Рабочая длина шпонки составляет lp= l- b= 30- 8= 22 мм. Проверяем шпонку на смятие, МПа sсм= 4Мкр1/(hlpdb)= 4*44,8*103/(7*22*30)= 38,8 МПа < [ sсм ]= 80…150 МПа.
Муфта Из справочника [5] для диаметра 30мм выбираем призматическую шпонку такую же, как и для шестерни. Ее напряженность такая же как и на шестерне.
4.2. Расчет выходного вала (см. рис.П2.4) 4.2.1. Определение диаметров под шестерню, подшипник и муфту вала. Крутящий момент Мкр2 = 172 Нм. Окружная сила Ft2=2Мкр2/dm2= 2*172*103/184=1869H. Радиальная сила Fr2= Ft2tga cosd2 =1869*0,364*0,243= 165,4 Н, Осевая сила Fa2= Ft2tga sind2 =1869*0,364*0,97= 659,9 Н. Сила на муфте Fм2= 250*(Мкр2)1/2 = 250*(172)1/2= 3278,7 Н. Принимаем материал вала - сталь 45, улучшенная с пределом прочности sв = 750 МПа; пределом текучести sт = 450 МПа. Принимаем допускаемое напряжение на кручение [t] = 12 МПа. Тогда предварительный диаметр вала d= {Мкр1/(0,2[t])}1/3 = {172*103 /(0,2*12)}1/3 = 41,5 мм Принимаем: Посадка колеса на диаметр dк2= 45 мм, длина зубьев колеса bw = 31,6 мм. Диаметр в месте посадки подшипников dп2= 40 мм; в месте посадки муфты dм2= 35 мм. 4.2.2. Выбор подшипников и определение схемы размещения опор.
Предварительно выбираем роликовые конические однорядные подшипники 20007308, имеющим Са= 59780 Н, Со= 45080 Н. По ним оцениваем конструкцию вала с осевыми размерами. Схема размещения опор приведена на рис. П2.4. Расстояния между опорами и точками приложения сил, определенные из принципа подобия и с учетом размеров колес, составляют, мм: a2= 70; b2=35; c2= 40; l2= a2+ b2=105. 4.2.3. Определение реакций опор. Примем, что радиальная нагрузка на валу Fm2= 250 (Мкр2)1/2 = 250 *1721/2= =3278,7 Н. Изгибающий момент Ma= 0,5Fa2 *dm2= 0,5*659,9 * 184= 6,07*104,Нмм Реакции в опорах от сил в вертикальной плоскости А21=(Frb2 - Ma)/l2 = (165,4*35- 6,07*104)/105= - 522,9 Н; B21= (Fra2 + Ma)/l2 = (165,4 *70+ 6,07*104)/105= 688,4 Н.
Реакция от сил Ft и Fm, действующих в горизонтальной плоскости B22= [Ft2 a2 - Fm2 (c2 +l2)]/l2 = [1869 * 70 - 3278,7(40+ 105)]/105= -3281,7 H; А22= (Ft2 b2 + Fm2 c2)/l2= 1872 Н. 4.2.4. Определение напряжений и запасов по прочности. Для 1-го сечения изгибающий момент равен М21= {(A21 a2)2+ (A22a2)2}1/2 = 70*(522,92+ 18722)1/2= 136,06*103Нмм. Напряжение изгиба sи= М21/(0,1* d3 к2) = 136,06*103/(0,1*453)= 14,93 МПа Напряжение кручения t = Мкр2/(0,2* d3 к2) = 172*103/(0,2*453)= 9,44МПа s-1= 0,4 sв = 0,4*750= 300МПА. t-1= 0,2sв = 150 МПа, tв= 0,6sв= 450 МПа. По рекомендациям [4] принимаем sа=sи; ta=tm= 0,5t; ys=0; yt=0,05 По графику (рис. 15.5 кривая 2) Kd= 0,75. По графику (рис. 15.6) для шлифованного вала КF= 1. По табл. 15.1 для шпоночного паза Кs = 2,0; Кt=1,7. Находим запас сопротивления усталости по изгибу Ss=s-1/[saKs/(KdKF)+yssm] = 300*0,75/(14,93*2)= 7,53; St= t-1/[ta Кt/(KdKF)+ yttm]= 150/[4,72*1,7/(0,75)+ 0,05*4,72]= 13,72
Откуда при совместном действии сил S= Ss* St/(S2t+ S2s)1/2 = 6,6> 1,5.
Рис. П2.4
Для второго сечения изгибающий момент равен Ми2@ Fm2c2 = 3278,7*40= =1,31*105Нмм Напряжения изгиба sи2= Ми2/(0,1*dп2 3) = 1,31*105/(0,1*403)= 20,49МПа. кручения t2= Мкр2/(0,2* dп2 3) = 172*103/(0,2*403)=13,4 МПа.. Принимаем радиус галтели перехода от диаметра под муфту к диаметру вала r = 2 мм, тогда r/d=2/45=0,044 и находим по (табл. 15.1 [4]). По табл. 15.1[4] находим Ks=2,1, Kt= 1,5 Определяем запасы сопротивления усталости по изгибу Ss= s-1/[saKs/(KdKF)+ yssm] = 300*0,75/(20,49*2,1)= 5,22. по кручению St= t-1/[taKt/(KdKF)+ yttm] = 150/[6,72*1,5/(0,75)+ 0,05*6,72]= 10,88. S= Ss* St/(S2t+ S2s)1/2 = 5,22* 10,88.(5,222+ 10,882)1/2 = 4,71>1,5. Больше напряжено 2-е сечение- под подшипником. Проверяем статическую прочность при перегрузках, когда напряжения удваиваются sэк= (s2и2+ 3t2 2)1/2= [(2*20,492+ 3(2*13,4)2]1/2= 61,92 МПа. Должно быть меньше [s]@ 0,8sт= 0,8* 450= 360 МПа. По прочности удовлетворяет.
4.2.5. Проверяем жесткость вала. Наиболее опасным здесь является прогиб вала под колесом. Для определения прогиба вычислим момент инерции сечения вала J= pd4п2/64= p*454/64= 2,01*105, мм4 Прогиб в вертикальной плоскости от силы Fr2 равен мм yв = Fr2a2 2 b2 2/(3EJ l2) = 165,4*702 352/(3*2,1*105*2,01*105*105)= 7,47*10-5 мм От момента Ма прогиб равен нулю. Прогиб в горизонтальной плоскости от сил Ft и Fм равен yг= Ft(a2*b2)2/(3EJ l2) + Fмс2 a2 (l2 2- a2 2)/(6EJ l2) = = 1869* 702 352/(3*2,1*105*2,01*105*105)+ 3278,7*40*70*(1052- - 702)/ (6*2,1*105*2,01*105*105)= 1,31*10-3+ 3,37*10-5= 8,65*10-4 Суммарный прогиб равен, мм Y= (y2в+ y2г)1/2 = [(0,747*10-4)2 +(8,65*10-4)2]1/2 = 8,68*10-4мм. Допускаемый прогиб [y]@ 0,01*m= 0,01*2= 2*10-2мм. Следовательно, прогиб меньше допускаемого. 4.2.6.Определение резонансных частот. Сила веса колеса Gш = 9,8* 7,8*10-6* 0,786*d2m2b’ = 9,8* 7,8*10-6* 0,786* 1842* 8,98= 18,3 H. Здесь ширина колеса определялась из выражения b’@1,1 b*cosd2= 1,1*33,6*0,243= 8,98 мм. (Для цилиндрических колес при cosd2 =1 можно приближено брать b@1,1 bw, хотя в принципе следует учитывать размеры ступицы колеса, его конфигурацию. Вместо dm2 необходимо подставлять делительный диаметр колеса). Прогиб вала от веса колеса, мм yнш=Gшa2b2/(3E J l)= 18,3*702 352/(3*2,1*105*2,01*105*105)= 8,26*10-6мм. Резонансные частоты круговая wr1= (g/yнш)1/2 = (9800/8,26*10-6)1/2= 3,44*104 рад/сек. периодическая nr= wr1/(2p)= 5,47*103Гц. Первая критическая частота вращения, при которой возможен резонанс, равна nкр1= 60nr= 328,2*103 об/мин. Вторая критическая частота вращения от зубцовых колебаний nкр2= 60 nr / z1= 60 * 5,47*103/92= 3567 об/мин. Крутильная упругость вала Jк= 2*(b2 +c2)/[8*105(dсв2/2)4] = 2*(35+40)/[8*105*(36,67/2)2]= 1,66*10-9 1/(Нмм) где dсв2@ [(dм2+ c2) dм2 2+ b2dn 22)/(dм2+ b2 + c2)]1/2= 36,67 мм- средний диаметр вала. Маховой момент колеса Jмах= mшR2/2 = (Gш/g)(dm2/2)2/2= (18,3/9800)*(184/2)2/2= 7,9 Нммсек2 Крутильные резонансные частоты круговая wkr= (JмахJк)-1/2 = (7,9*1,66*10-9)-1/2= 8732 рад/сек; периодическая nkr= wkr/(2p)= 1390,4Гц. Третья критическая частота по крутильным колебаниям nкр3= wkz*60/(2p) = 8732*60/6,28 = 83427 об/мин. Четвертая критическая частота вращения от зубцовых колебаний nк42= 60 nkr / z2= 60 * 1434/92= 906,8 об/мин. Критические частоты вращения не совпадают с частотой вращения выходного вала.
4.2.7. Проверочный расчет подшипников качения на выходном валу. Выбранные в п.п. 4.2.2 подшипники № 2007208 имеют Са= 59780 Н, Со= 45080 Н Ресурс подшипников, Lh0= 24000 час. Находим Fa2/C0= 659,9/45080= 0,0146. Суммарные радиальные составляющие, Н Fr1= (A21+ A22)1/2 = (829,92+ 1872,22)1/2= 2047; Fr2= (B21+ B22)1/2 = (688,42+ 3281,72)1/2 = 3353. По табл. 16.5 [1] находим e= 1,5*ctg a. Из каталога следует a =15° и e=5,56 и далее при V=1 Fa2/(VFrmax)= 659,9/3353= 0,197 При этом X=1, Y=0. По рекомендациям [1] принимаем Кs= 1,3; Кт= 1. Тогда радиальная нагрузка Pr= Frmax*1,3= 1,3*3353= 4358 H. Используя графики типовых режимов (рис. 8.42 [1]), эквивалентную долговечность определим, час LhE= KHELh0=0,25*24000= 6000. Находим эквивалентный ресурс LE = 60*10-6*n*LhE= 60*10-6*240*6000= 86,4 млн. обор. При а1=1, а2=1, р=3,33 определим динамическую грузоподъемность C= Pr [LE /(a1a2)]1/P = 4358*(86,4)1/3,33= 16605 H. Проверяем подшипник по статической грузоподъемности c учетом 2-х кратной перегрузки. P0= X0Fr+ Y0Fa = 2(0,6 Fr max+0,5Fa2)= 2*(0,6*3353+ 0,5*659,9)= 4683,5Н Сравниваем с паспортной составляющей. При необходимости уточняем подшипник и выбираем Са, С0. Здесь этого не требуется. 4.2.8. Выбор и расчет шпонок Муфта Из справочника [5] для диаметра 35 мм выбираем призматическую шпонку 10х8х35 ГОСТ 23360- 78 из чистотянутой стали с пределом прочности свыше 600 МПа. Рабочая длина шпонки составляет lp= l- b= 35- 10= 25 мм. Проверяем шпонку на смятие, МПа sсм= 4Мкр1/(hlpdb)= 4*172*103/(8*25*35)= 98,3 МПа < [ sсм ]= 80…150 МПа.
Колесо Из справочника [5] для диаметра 45 мм выбираем призматическую шпонку 14х9х40 ГОСТ 23360- 78 из чистотянутой стали с пределом прочности свыше 600 МПа. Рабочая длина шпонки составляет lp= l- b= 40- 14= 26 мм. Проверяем шпонку на смятие, МПа sсм= 4Мкр1/(hlpdb)= 4*172*103/(9*26*45)= 65,3 МПа < [ sсм ]= 80…150 МПа.
|