Ситуация 2
ТРЕБУЕТСЯ: 1.Составить математическую модель планирования производства, записав соответствующую задачу ЗЛП в стандартном виде. Указать смысл всех используемых обозначений и математических выражений. Известны: bi (i = 1,2,3,...,m) — запасы каждого i-го вида ресурса; aij (i = 1,2,3,...,m; j=1,2,3,...,n) — затраты каждого i-го вида ресурса на производство единицы объема j-го вида продукции; cj (j = 1,2,3,...,n) — прибыль от реализации единицы объема j-го вида продукции. Требуется составить план производства продукции, который обеспечивает максимум прибыли при заданных ограничениях на ресурсы (сырье). Введем вектор переменных X=(X1, X2,...,Xn), где xj (j = 1,2,...,n) — объем производства j-го вида продукции. Затраты i-го вида ресурса на изготовление данного объема xj продукции равны aijxj, поэтому ограничение на использование ресурсов на производство всех видов продукции имеет вид: Математическая модель имеет вид: F=4x1+7x2 + x3→max
2. Привести задачу к каноническому виду. F=4x1+7x2 + x3→max
х3
F=4x1+7x2+12-2х1-2х2 => F=2x1+5x2+12→max 3.Найти графическим методом оптимальный план выпуска продукции.
gradF = (2;5)
Ответ: координаты максимальной точки B(0;5) 3.Привести задачу к каноническому виду.
4.Найти решение полученной задачи симплекс-методом. F= -4x1-7x2-x3
Оптимальный план можно записать так: 6. Excel
7. Анализ результатов Предприятию «P1 & P2» не выгоден переход от старой программы к новой, т.к прибыль уменьшилась.
|

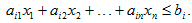



 12-2х1-2х2
12-2х1-2х2



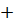 M
M  4x1+7x2 + x3
4x1+7x2 + x3 

 M
M
 - 1
- 1 




