Управление запасами является ключевой активностью, составляющей наиболее важную сферу логистического менеджмента фирмы, как с точки зрения трудоемкости, так и связанных с нею затрат. Для эффективного функционирования логистической системы необходимо создавать страховой запас, предназначенный для элиминирования логистических и финансовых рисков, связанных с непредвиденными колебаниями спроса на готовую продукцию, невыполнением договорных обязательств по поставкам материальных ресурсов, сбоями в производственно-технологических циклах и другими непредвиденными обстоятельствами. Так как в любых запасах замораживаются большие финансовые средства, поэтому определение оптимального уровня страхового запаса является актуальной задачей в логистике.
На логистические системы управления материальными запасами оказывают влияние множество факторов, приводящие к колебаниям параметров системы, которые, таким образом, становятся случайными величинами. Случайной величиной может быть потребление и поступление материальных ресурсов или время выполнения заказа. Поскольку определяющим фактором в моделях управления запасами является спрос, то проведем анализ случайных величин на примере этого фактора.
Пусть спрос на продукцию предприятия или расход материальных ресурсов – случайная величина с математическим ожиданием 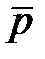 и конечной дисперсией
и конечной дисперсией  .
.
Чтобы избежать дефицита в системе при случайных колебаниях спроса, предприятию необходимо иметь некоторый страховой запас 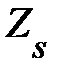 . Для бездефицитной работы логистической системы вероятность того, что спрос за время цикла между поставками не превысит величины, равной сумме оптимального размера заказа и страхового запаса
. Для бездефицитной работы логистической системы вероятность того, что спрос за время цикла между поставками не превысит величины, равной сумме оптимального размера заказа и страхового запаса  , должна быть достаточно велика. Эту вероятность называют коэффициентом надежности и обозначают через
, должна быть достаточно велика. Эту вероятность называют коэффициентом надежности и обозначают через 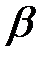 . Обычно требуются, чтобы коэффициент надежности был равен 0,9; 0,95 или 0,99. Иногда удобнее использовать коэффициент риска
. Обычно требуются, чтобы коэффициент надежности был равен 0,9; 0,95 или 0,99. Иногда удобнее использовать коэффициент риска 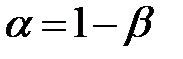 . То есть, если
. То есть, если 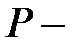 спрос между двумя последовательными моментами размещения заказа, то размер страхового запаса
спрос между двумя последовательными моментами размещения заказа, то размер страхового запаса  определяется таким образом, чтобы вероятность истощения запасав в течение цикла не превышала заданной величине
определяется таким образом, чтобы вероятность истощения запасав в течение цикла не превышала заданной величине 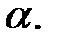
Предположим, что  – плотность распределения вероятностей спроса в течение этого срока, а вероятность истощения запаса в течение цикла не должна превышать. Тогда размер страхового запаса определяется из условия следующей формулы:
– плотность распределения вероятностей спроса в течение этого срока, а вероятность истощения запаса в течение цикла не должна превышать. Тогда размер страхового запаса определяется из условия следующей формулы:
 , (70)
, (70)
Если распределение спроса подчинена нормальному закону, то функция плотности распределения имеет вид:
 , (71)
, (71)
Введем обозначения:
 (72)
(72)
где 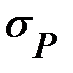 - среднеквадратическое отклонение случайной величины спроса, рассчитываемое по формуле:
- среднеквадратическое отклонение случайной величины спроса, рассчитываемое по формуле:
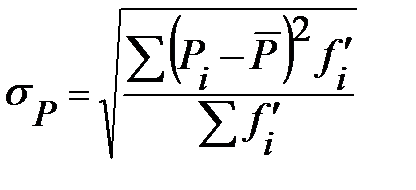 , (73)
, (73)
где 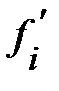 - частота, с которой наблюдается величина спроса
- частота, с которой наблюдается величина спроса 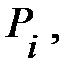
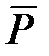 - средняя величина спроса за исследуемый период то есть:
- средняя величина спроса за исследуемый период то есть:
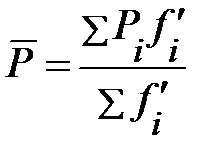 , (74)
, (74)
С учетом этих обозначений функция и плотность вероятности примут вид соответственно:
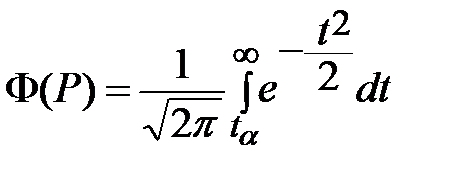 , (75)
, (75)
 . (76)
. (76)
Задача нахождения оптимально страхового запаса при нормальном распределении вероятностей величины спроса формулируется следующим образом: по заданному значению коэффициента риска  найти значение величины
найти значение величины  , для которого выполняется равенство:
, для которого выполняется равенство:
 , (77)
, (77)
Решение этого уравнения относительно 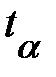 по заданному коэффициенту риска находится из таблиц нормального распределения. Поскольку риск будет существовать, то
по заданному коэффициенту риска находится из таблиц нормального распределения. Поскольку риск будет существовать, то  . Учитывая, что
. Учитывая, что  , то страховой запас должен быть, по меньшей мере
, то страховой запас должен быть, по меньшей мере 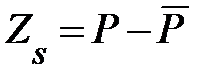 . Таким образом, страховой запас определяется по следующей формуле:
. Таким образом, страховой запас определяется по следующей формуле:
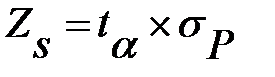 , (78)
, (78)
где  определяется по таблице функции Лапласа (приложение В).
определяется по таблице функции Лапласа (приложение В).
При распределении спроса по закону Пуассона функция плотности вероятностей имеет вид:
 , (79)
, (79)
А величина страхового запаса находиться по формуле:
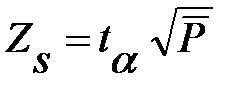 , (80)
, (80)
где  определятся по специальным таблицам теории вероятностей (приложение В).
определятся по специальным таблицам теории вероятностей (приложение В).
Для экспоненциального (показательного) распределения с функцией плотности вероятности:
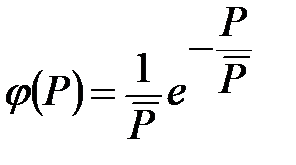 , (81)
, (81)
А величина страхового запаса находиться по формуле:
 , (82)
, (82)
Порядок определения страхового запаса:
1) Выдвигается гипотеза о законе распределения случайной величины спроса.
2) Выдвинутую гипотезу нужно либо подтвердит, либо опровергнуть.
Для этого можно воспользоваться критерием Пирсона:
 , (83)
, (83)
где 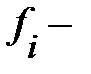 теоретические частоты;
теоретические частоты;
 эмпирические частоты.
эмпирические частоты.
Для нормального закона распределения:
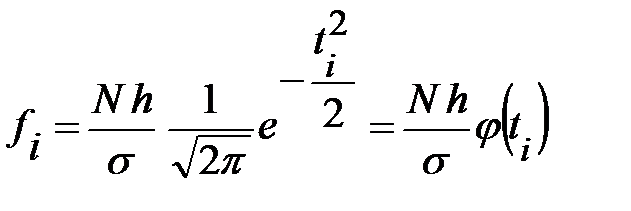 , (84)
, (84)
где  длина шага между соседними значениями спроса;
длина шага между соседними значениями спроса; 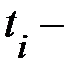 нормированная случайная величина спроса, рассчитываемая по формуле:
нормированная случайная величина спроса, рассчитываемая по формуле:
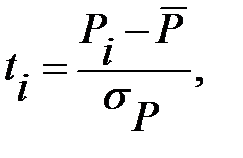 (85)
(85)
Для распределения Пуассона теоретические частоты вычисляют по формуле:
 , (86)
, (86)
Для экспоненциального распределения:
 , (87)
, (87)
По таблице критических точек распределения 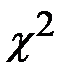 по заданному уровню значимости
по заданному уровню значимости 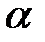 и числу степеней свободы
и числу степеней свободы 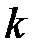 определяется критическое значение критерия Пирсона
определяется критическое значение критерия Пирсона 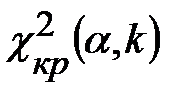 . Количество степеней свободы для нормального распределения
. Количество степеней свободы для нормального распределения  (
(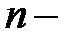 число интервалов), для пуассоновского и экспоненциального
число интервалов), для пуассоновского и экспоненциального 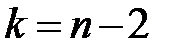 . Если
. Если  , то выдвинутая гипотеза принимается, в противном случае – отвергается.
, то выдвинутая гипотеза принимается, в противном случае – отвергается.
3) После выявления закона распределения остается найти величину страхового запаса, т. е. воспользоваться формулами (78) или (80) или (82).
 Таким образом, осуществляется определение страхового запаса.
Таким образом, осуществляется определение страхового запаса.
Пример. На фирме для производство готовой продукции А используется сырье (полуфабрикат). Временное отсутствие, которого, приводит к срыву производства продукции, поэтому его дефицит не допустим. Сведения о ежедневной потребности данного сырья представлен в табл. 6.10.
Таблица 6.10
Исходные данные
| № периода
| Ежедневное потребление
| № периода
| Ежедневное потребление
| № периода
| Ежедневное потребление
| № периода
| Ежедневное потребление
| № периода
| Ежедневное потребление
|
|
|
|
|
|
|
|
|
|
|
|
Необходимо определить величину страхового запаса, гарантирующего бесперебойное функционирование фирмы с вероятностью 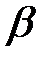 =0,95.
=0,95.
Решение. На первом этапе необходимо преобразовать исходную выборку в статистически группированный интервальный ряд. Для этого необходимо выделить десять интервалов. Преобразование исходной выборки в статистически интервальный ряд выполняется в следующем порядке:
1) Определим размах выборки 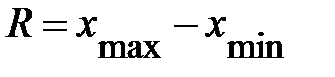 , где
, где 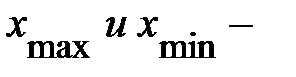 максимальное и минимальное значение ежесуточной потребности в материальном ресурсе. Тогда
максимальное и минимальное значение ежесуточной потребности в материальном ресурсе. Тогда

2) Вычислим величину интервала:

3) Рассчитаем границы интервалов. При этом нижняя граница первого интервала будет равняться минимальному значению группировочного признака (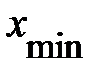 ). Для того чтобы найти верхнюю границу этого интервала необходимо нижней границе прибавить величину интервала (
). Для того чтобы найти верхнюю границу этого интервала необходимо нижней границе прибавить величину интервала (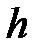 ). Это будет нижней границей второго интервала. Далее прибавив величину интервала, получим верхнюю границу и т. д.
). Это будет нижней границей второго интервала. Далее прибавив величину интервала, получим верхнюю границу и т. д.
Далее определяются эмпирические частоты (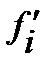 ), как количество группировочного признака в каждом интервале. Для определения среднесуточного расхода материального ресурса и среднеквадратического отклонения расхода вычислим середину интервала, как полусумма границ каждого интервала. Результаты этих и других операции сведены в таблицу 6.11.
), как количество группировочного признака в каждом интервале. Для определения среднесуточного расхода материального ресурса и среднеквадратического отклонения расхода вычислим середину интервала, как полусумма границ каждого интервала. Результаты этих и других операции сведены в таблицу 6.11.
Таблица 6.11
Интервальный статистически ряд
| № интервала
| Интервал интенсивности потребления

| Эмпирические частоты

| Середина интервала
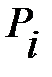
| 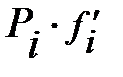
| 
|
|
| 171,0 – 176,9
|
| 173,95
| 869,75
| 3218,184
|
|
| 176,9 – 182,8
|
| 179,85
| 1079,10
| 2274,485
|
|
| 182,8 – 188,7
|
| 185,75
| 5201,00
| 5156,057
|
|
| 188,7 – 194,6
|
| 191,65
| 11307,35
| 3470,905
|
|
| 194,6 – 200,5
|
| 197,55
| 12445,65
| 618,904
|
|
| 200,5 – 206,4
|
| 203,45
| 14241,50
| 1193,983
|
|
| 206,4 – 212,3
|
| 209,35
| 9211,40
| 4426,440
|
|
| 212,3 – 218,2
|
| 215,25
| 3444,00
| 4060,238
|
|
| 218,2 – 224,1
|
| 221,15
| 1769,20
| 3812,391
|
|
| 224,1 – 230,0
|
| 227,05
| 227,05
| 768,953
|
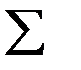
| -
|
| -
| 59796,00
| 29000,540
|
На основании этой таблицы по формулам (74) и (73) определим среднесуточный расход материального ресурса и среднеквадратическое отклонение расхода от среднего. Они соответственно равны: 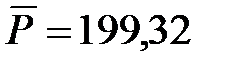 ;
; 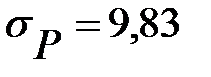 .Далее выдвигается гипотеза о нормальном законе распределения расхода данного материального ресурса. Выдвинутую гипотезу необходимо подтвердит или опровергнут. Для этого воспользуемся критерием Пирсона (83). Вычисление элементов критерия Пирсона сведем в таблицу 6.12.
.Далее выдвигается гипотеза о нормальном законе распределения расхода данного материального ресурса. Выдвинутую гипотезу необходимо подтвердит или опровергнут. Для этого воспользуемся критерием Пирсона (83). Вычисление элементов критерия Пирсона сведем в таблицу 6.12.
Таблица 6.12
Вычисление элементов критерия Пирсона
| Номер интервала
| Середина интервала
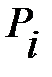
| Частота

| 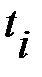
| 
| 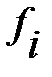
| 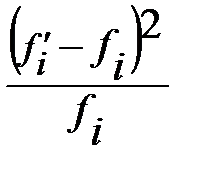
|
|
| 173,95
|
| -2,58
| 0,0143
| 2,51
| 2,47
|
|
| 179,85
|
| -1,98
| 0,0562
| 10,12
| 1,68
|
|
| 185,75
|
| -1,38
| 0,1539
| 27,71
| 0,00
|
|
| 191,65
|
| -0,78
| 0,2943
| 52,99
| 0,68
|
|
| 197,55
|
| -0,18
| 0,3925
| 70,67
| 0,83
|
|
| 203,45
|
| 0,42
| 0,3653
| 65,78
| 0,27
|
|
| 209,35
|
| 1,02
| 0,2371
| 42,69
| 0,04
|
|
| 215,25
|
| 1,62
| 0,1074
| 19,34
| 0,58
|
|
| 221,15
|
|  2,22 2,22
| 0,0339
| 6,10
| 0,59
|
|
| 227,05
|
| 2,82
| 0,0075
| 1,35
| 0,09
|
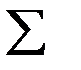
|
|
| -
|
|
| 7,23
|
Примечание. Значение функции плотности вероятностей  определяется по таблице (приложение А).
определяется по таблице (приложение А).
Сравним эмпирические и теоретические частоты. Наблюдаемые значения критерия Пирсона 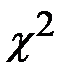 =7,23. Из таблицы критических точек распределения
=7,23. Из таблицы критических точек распределения 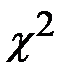 (приложение Б) найдем
(приложение Б) найдем 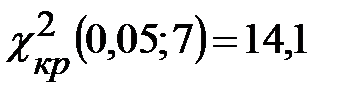 . Так как
. Так как 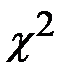 <
< 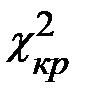 , то предложение о нормальном законе распределения спроса подтвердилось. Страховой запас
, то предложение о нормальном законе распределения спроса подтвердилось. Страховой запас 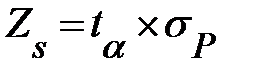 . Величину
. Величину 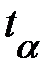 находим из таблицы приложение В. Для
находим из таблицы приложение В. Для  ,
,  =1,96. Итак,
=1,96. Итак, 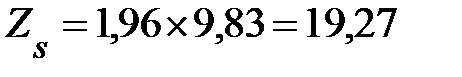 . Таким образом, определяется страховой запас для функциональных подсистем логистической системы.
. Таким образом, определяется страховой запас для функциональных подсистем логистической системы.

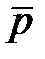 и конечной дисперсией
и конечной дисперсией  .
.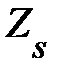 . Для бездефицитной работы логистической системы вероятность того, что спрос за время цикла между поставками не превысит величины, равной сумме оптимального размера заказа и страхового запаса
. Для бездефицитной работы логистической системы вероятность того, что спрос за время цикла между поставками не превысит величины, равной сумме оптимального размера заказа и страхового запаса  , должна быть достаточно велика. Эту вероятность называют коэффициентом надежности и обозначают через
, должна быть достаточно велика. Эту вероятность называют коэффициентом надежности и обозначают через 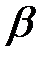 . Обычно требуются, чтобы коэффициент надежности был равен 0,9; 0,95 или 0,99. Иногда удобнее использовать коэффициент риска
. Обычно требуются, чтобы коэффициент надежности был равен 0,9; 0,95 или 0,99. Иногда удобнее использовать коэффициент риска 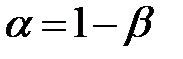 . То есть, если
. То есть, если 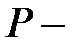 спрос между двумя последовательными моментами размещения заказа, то размер страхового запаса
спрос между двумя последовательными моментами размещения заказа, то размер страхового запаса  определяется таким образом, чтобы вероятность истощения запасав в течение цикла не превышала заданной величине
определяется таким образом, чтобы вероятность истощения запасав в течение цикла не превышала заданной величине 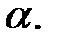
 – плотность распределения вероятностей спроса в течение этого срока, а вероятность истощения запаса в течение цикла не должна превышать. Тогда размер страхового запаса определяется из условия следующей формулы:
– плотность распределения вероятностей спроса в течение этого срока, а вероятность истощения запаса в течение цикла не должна превышать. Тогда размер страхового запаса определяется из условия следующей формулы: , (70)
, (70) , (71)
, (71) (72)
(72)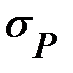 - среднеквадратическое отклонение случайной величины спроса, рассчитываемое по формуле:
- среднеквадратическое отклонение случайной величины спроса, рассчитываемое по формуле: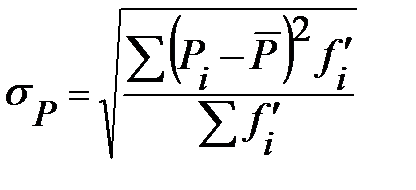 , (73)
, (73)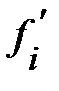 - частота, с которой наблюдается величина спроса
- частота, с которой наблюдается величина спроса 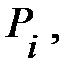
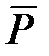 - средняя величина спроса за исследуемый период то есть:
- средняя величина спроса за исследуемый период то есть: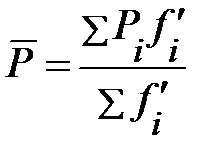 , (74)
, (74)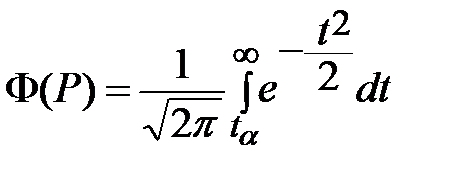 , (75)
, (75) . (76)
. (76) найти значение величины
найти значение величины  , для которого выполняется равенство:
, для которого выполняется равенство: , (77)
, (77)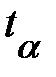 по заданному коэффициенту риска находится из таблиц нормального распределения. Поскольку риск будет существовать, то
по заданному коэффициенту риска находится из таблиц нормального распределения. Поскольку риск будет существовать, то  . Учитывая, что
. Учитывая, что  , то страховой запас должен быть, по меньшей мере
, то страховой запас должен быть, по меньшей мере 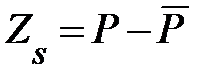 . Таким образом, страховой запас определяется по следующей формуле:
. Таким образом, страховой запас определяется по следующей формуле: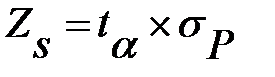 , (78)
, (78) определяется по таблице функции Лапласа (приложение В).
определяется по таблице функции Лапласа (приложение В). , (79)
, (79)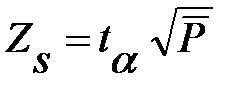 , (80)
, (80) определятся по специальным таблицам теории вероятностей (приложение В).
определятся по специальным таблицам теории вероятностей (приложение В).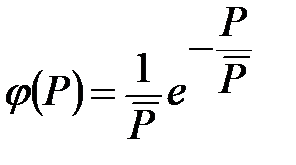 , (81)
, (81) , (82)
, (82) , (83)
, (83)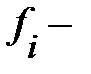 теоретические частоты;
теоретические частоты; эмпирические частоты.
эмпирические частоты.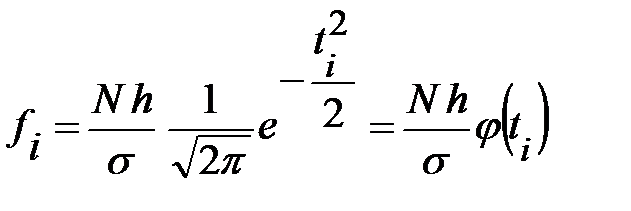 , (84)
, (84) длина шага между соседними значениями спроса;
длина шага между соседними значениями спроса; 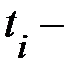 нормированная случайная величина спроса, рассчитываемая по формуле:
нормированная случайная величина спроса, рассчитываемая по формуле: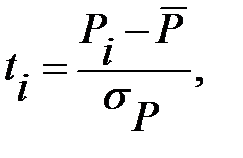 (85)
(85) , (86)
, (86) , (87)
, (87)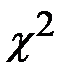 по заданному уровню значимости
по заданному уровню значимости 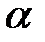 и числу степеней свободы
и числу степеней свободы 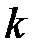 определяется критическое значение критерия Пирсона
определяется критическое значение критерия Пирсона 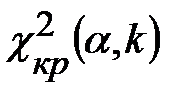 . Количество степеней свободы для нормального распределения
. Количество степеней свободы для нормального распределения  (
(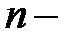 число интервалов), для пуассоновского и экспоненциального
число интервалов), для пуассоновского и экспоненциального 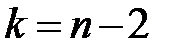 . Если
. Если  , то выдвинутая гипотеза принимается, в противном случае – отвергается.
, то выдвинутая гипотеза принимается, в противном случае – отвергается. Таким образом, осуществляется определение страхового запаса.
Таким образом, осуществляется определение страхового запаса.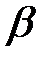 =0,95.
=0,95.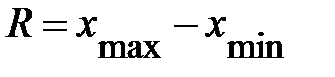 , где
, где 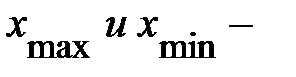 максимальное и минимальное значение ежесуточной потребности в материальном ресурсе. Тогда
максимальное и минимальное значение ежесуточной потребности в материальном ресурсе. Тогда

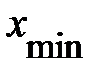 ). Для того чтобы найти верхнюю границу этого интервала необходимо нижней границе прибавить величину интервала (
). Для того чтобы найти верхнюю границу этого интервала необходимо нижней границе прибавить величину интервала (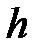 ). Это будет нижней границей второго интервала. Далее прибавив величину интервала, получим верхнюю границу и т. д.
). Это будет нижней границей второго интервала. Далее прибавив величину интервала, получим верхнюю границу и т. д.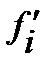 ), как количество группировочного признака в каждом интервале. Для определения среднесуточного расхода материального ресурса и среднеквадратического отклонения расхода вычислим середину интервала, как полусумма границ каждого интервала. Результаты этих и других операции сведены в таблицу 6.11.
), как количество группировочного признака в каждом интервале. Для определения среднесуточного расхода материального ресурса и среднеквадратического отклонения расхода вычислим середину интервала, как полусумма границ каждого интервала. Результаты этих и других операции сведены в таблицу 6.11.

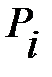
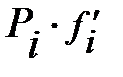

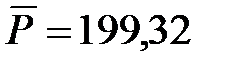 ;
; 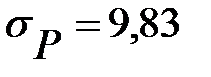 .Далее выдвигается гипотеза о нормальном законе распределения расхода данного материального ресурса. Выдвинутую гипотезу необходимо подтвердит или опровергнут. Для этого воспользуемся критерием Пирсона (83). Вычисление элементов критерия Пирсона сведем в таблицу 6.12.
.Далее выдвигается гипотеза о нормальном законе распределения расхода данного материального ресурса. Выдвинутую гипотезу необходимо подтвердит или опровергнут. Для этого воспользуемся критерием Пирсона (83). Вычисление элементов критерия Пирсона сведем в таблицу 6.12.

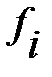
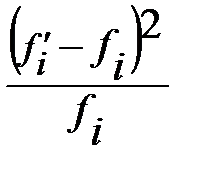
 2,22
2,22
 определяется по таблице (приложение А).
определяется по таблице (приложение А).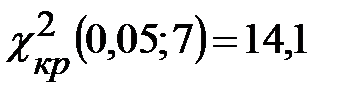 . Так как
. Так как 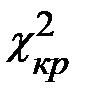 , то предложение о нормальном законе распределения спроса подтвердилось. Страховой запас
, то предложение о нормальном законе распределения спроса подтвердилось. Страховой запас 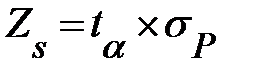 . Величину
. Величину 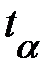 находим из таблицы приложение В. Для
находим из таблицы приложение В. Для  ,
,  =1,96. Итак,
=1,96. Итак, 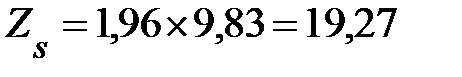 . Таким образом, определяется страховой запас для функциональных подсистем логистической системы.
. Таким образом, определяется страховой запас для функциональных подсистем логистической системы.


