Транспортная модель
Транспортная модель (транспортная задача) используют при рассмотрении различных практических ситуаций в логистическом управлении, связанных: с составлением наиболее экономичного плана перевозок продукции, управление запасами, назначением служащих на рабочее места, оборотом наличного капитала и многими другими. Кроме того, модель можно изменить, чтобы она учитывала перевозку нескольких видов продукции. В то же время транспортная модель и ее обобщение представляют собой частные случаи сетевых моделей. Транспортная задача по существу представляет собой задачу линейного программирования, которую можно решать симплекс – методом. Однако специфическая структура условий задачи позволяет использовать более эффективные вычислительные алгоритмы. Сущность транспортной задачи линейного программирования состоит в наивыгоднейшем прикреплении поставщиков однородного продукта ко многим потребителям этого продукта. На практике постоянно возникает необходимость решения таких задач, особенно когда количество пунктов отправления и получения грузов увеличивается. Условие транспортной задачи обычно записывается в виде матрицы, в которой потребители однородного груза размещаются по столбцам, а поставщики - по строкам. В последнем столбце матрицы проставляют запас груза, имеющийся у каждого поставщика, а в последней строке - потребность в нем потребителей. На пересечении строк со столбцами (в клетках матрицы) записывают размер поставки, а также расстояние пробега по всем возможным маршрутам время доставки груза или затраты на перевозку единицы груза по этим маршрутам. Постановка задачи и ее математическая модель. Некоторый однородный продукт, сосредоточенный у т поставщиков в количестве

Рис. 7.1. Транспортная модель
На рис. 7. 1. изображена транспортная модель в виде сети с т поставщиками некоторого однородного груза и п потребителями этого груза. При этом поставщикам груза и потребителям соответствуют вершины сети. Дуга, соединяющая поставщик груза с потребителем, представляет условный маршрут, по которому перевозится продукция. Количество продукции, производимой поставщиком Запишем математическую модель задачи: 1) Объем поставок
2) Объем поставок
3) Запас груза у поставщиков должен равняться суммарному спросу потребителей:
4) Размер поставок должен выражаться неотрицательным числом:
5) общая сумма затрат на перевозку груза должна быть минимальной:
Поставленная в задаче цель может быть достигнута различными методами, например, методом северо-западного угла или методом потенциалов. Модель транспортной задачи линейного программирования так же может использоваться для планирования ряда операций, не связанных с перевозкой грузов. Так, с ее помощью решаются задачи по оптимизации размещения производства, топливно-энергетического баланса, планов загрузки оборудования распределения сельскохозяйственных культур по участкам различного плодородия и т. п. Поставленная транспортная задача линейного программирования называется сбалансированной транспортной моделью, так как объем запасов равняется объему заказов. В реальных ситуациях не всегда объем производства равен спросу, однако транспортную модель всегда можно сбалансировать. В случае превышения запас продукции над потребностью, т. е. если
(91)
а соответствующие стоимости перевозок Модель транспортной задачи представляет собой задачу линейного прогпаммирования и, етественно, ее можно решать с использованием метода последовательного улучшения плана или методом использованием метода последовательного улучшения оценок (симплексным методом). Но в этом случае основная трудность связана с числом переменных задачи Алгоритм метода потенциалов, (его называют еще модифицированным распределительным алгоритмом) начинает работу с некоторого опорного плана транспортной задачи (допустимого плана перевозок). Для построения опорного плана обычно используется один из двух методов: метод северо-западного угла или метод минимального элемента. На конкретной задаче рассмотрим метод северо-западного угла. Он позволяет найти некоторый допустимый план перевозок. Задача. На трех складах ( Таблица 7.2 Исходные данные для решения транспортной задачи
Найти допустимый план перевозок. Для решения задачи на первом этапе составляется система ограничений и целевая функция. Система ограничений в общем виде (для задачи) имеет вид:
причем Целевая функция затрат на перевозку, значение которой необходимо минимизировать при имеющихся ограничениях, выглядит следующим образом:
Далее перераспределяются объемы поставок грузов методом «северо-западного угла», т.е. первой заполняется верхняя левая (северо-западная) клетка исходной таблицы. Примем объем перевозки со склада В таблице 7.3. найдем «северо-западный угол» (теперь это клетка В нашей табл.7.3 найдем новый «северо-западный угол» (клетка В оставшейся части табл. № найдем новый «северо-западный угол» (клетка Результаты проведенных операций сведены в табл. 7.3.
Таблица 7.3 Распределение поставок
В результате получили опорный план
В результате дальнейших вычислений мы получим оптимальное минимальное значение целевой функции. Расчеты громоздки, но легко реализуются с использованием компьютерных программ.
|

 (
( ), необходимо доставить п потребителям в количестве
), необходимо доставить п потребителям в количестве  (
( ). Известно стоимость
). Известно стоимость 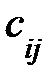 перевозки единицы груза от
перевозки единицы груза от  го поставщика
го поставщика  му потребителю. Необходимо составить план перевозок, имеющий минимальную стоимость. Основное предположение, используемое при построении модели, состоит в том, что величина транспортных расходов на каждом маршруте прямо пропорциональна объему перевозимой продукции. Модель транспортной задачи представлена на рис 7.1.
му потребителю. Необходимо составить план перевозок, имеющий минимальную стоимость. Основное предположение, используемое при построении модели, состоит в том, что величина транспортных расходов на каждом маршруте прямо пропорциональна объему перевозимой продукции. Модель транспортной задачи представлена на рис 7.1.

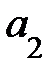




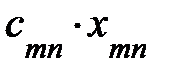
 , обозначено через
, обозначено через  , а количество продукции, потребляемой потребителем
, а количество продукции, потребляемой потребителем  через
через  ;
;  стоимость перевозки единицы продукции из
стоимость перевозки единицы продукции из  в
в  .
. го поставщика должен равняться количеству имеющегося у него груза:
го поставщика должен равняться количеству имеющегося у него груза: , (88)
, (88) му потребителю должен быть равен его спросу:
му потребителю должен быть равен его спросу: , (89)
, (89)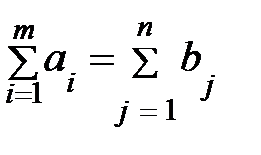 , (90)
, (90) ;(7.4).
;(7.4). (91)
(91)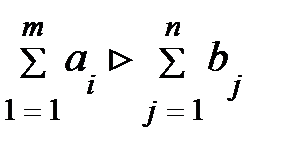 , вводится фиктивный (n+1) – й потребитель с потребностью
, вводится фиктивный (n+1) – й потребитель с потребностью
 считаются равными нулю. Аналогично, при
считаются равными нулю. Аналогично, при  , вводится фиктивный (m+1) – й поставщик с запасом груза
, вводится фиктивный (m+1) – й поставщик с запасом груза  а соответствующие стоимости перевозок
а соответствующие стоимости перевозок  считаются равными нулю. Этими действиями задача сводится к сбалансированной транспортной задаче, из оптимального плана которой, получается оптимальный план исходной задачи.
считаются равными нулю. Этими действиями задача сводится к сбалансированной транспортной задаче, из оптимального плана которой, получается оптимальный план исходной задачи.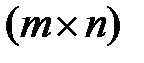 . Поэтому специальные алгоритмы, например, такие как метод потенциалов и венгерский метод, оказываются более эффективными.
. Поэтому специальные алгоритмы, например, такие как метод потенциалов и венгерский метод, оказываются более эффективными. ) имеется соответственно 140, 180 и 160 единиц однородного груза. Этот груз требуется перевести к пяти потребителям (
) имеется соответственно 140, 180 и 160 единиц однородного груза. Этот груз требуется перевести к пяти потребителям ( ) соответственно в количествах 60, 70, 120, 130, 100 единиц. Стоимость перевозки от складов к потребителям приведена в табл. 7.2. (в правом верхнем углу каждой клетки). Например, стоимость перевозки единицы груза со склада
) соответственно в количествах 60, 70, 120, 130, 100 единиц. Стоимость перевозки от складов к потребителям приведена в табл. 7.2. (в правом верхнем углу каждой клетки). Например, стоимость перевозки единицы груза со склада 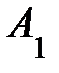 потребителю
потребителю  равна 2 у. е.
равна 2 у. е.
















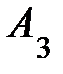


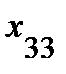



 для
для 

 = 2
= 2 
 + 3
+ 3 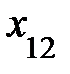 +4.
+4.  + 2
+ 2  + 4
+ 4  +
+  2
2 
 , (92)
, (92) к потребителю
к потребителю  максимально возможным из условий задачи и равным 60 ед. Потребитель
максимально возможным из условий задачи и равным 60 ед. Потребитель  полностью удовлетворил свою потребность, и поэтому графу «
полностью удовлетворил свою потребность, и поэтому графу «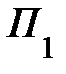 » в табл.7.3 можно исключить из дальнейшего рассмотрения.
» в табл.7.3 можно исключить из дальнейшего рассмотрения. )и укажем максимально возможное значение. Оно рассчитывается следующим образом: со склада
)и укажем максимально возможное значение. Оно рассчитывается следующим образом: со склада  уже перевезено 60 ед. груза, поэтому остаток на этом складе составляет 80 ед. (140—60). Вносим в клетку
уже перевезено 60 ед. груза, поэтому остаток на этом складе составляет 80 ед. (140—60). Вносим в клетку  вместо
вместо  значение, равное 70 ед. Потребитель
значение, равное 70 ед. Потребитель  полностью удовлетворил свою потребность, и поэтому графу «
полностью удовлетворил свою потребность, и поэтому графу « » в табл. 7.3. можно исключить из дальнейшего рассмотрения. Остаток продукции на складе
» в табл. 7.3. можно исключить из дальнейшего рассмотрения. Остаток продукции на складе  10 ед. (140 – 60 – 70) припишем потребителю
10 ед. (140 – 60 – 70) припишем потребителю 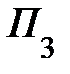 .Таким образом, весь груз со склада
.Таким образом, весь груз со склада  перевезен потребителям и первая строка табл. 7.3 исключается из дальнейшего рассмотрения.
перевезен потребителям и первая строка табл. 7.3 исключается из дальнейшего рассмотрения. )и укажем в нем максимально возможное значение это 110 ед. (120 – 10). Остаток продукции на складе
)и укажем в нем максимально возможное значение это 110 ед. (120 – 10). Остаток продукции на складе  70 ед. (180 – 110) припишем потребителю
70 ед. (180 – 110) припишем потребителю  . Тем самим потребитель
. Тем самим потребитель  полностью удовлетворил свою потребность, и поэтому графу «
полностью удовлетворил свою потребность, и поэтому графу « » в табл. 7.3 можно исключить из дальнейшего рассмотрения.
» в табл. 7.3 можно исключить из дальнейшего рассмотрения.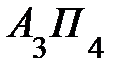 ) и укажем в нем максимально возможное значение это 60 ед. (130 – 70). Остаток продукции на складе
) и укажем в нем максимально возможное значение это 60 ед. (130 – 70). Остаток продукции на складе 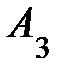 в количестве 100 ед. припишем потребителю
в количестве 100 ед. припишем потребителю  .
.





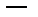


 (семь занятых клеток).
(семь занятых клеток). .
.


