В сети распределения
Одной из фундаментальных задач логистики является оптимальный выбор мест размещения и количество распределительных центров в распределительной сети.
В сети распределения продукции может быть несколько маршрутов (или физических каналов распределения продукции). Выбор нужного маршрута существенно влияет на уровень обслуживания потребителя и на уровень совокупных запасов в системе распределения. Это влияние должно тщательно учитываться при выборе метода распределения, включающего следующие аспекты:
- размещение складских помещений;
- способ транспортировки продукции;
- способ отгрузки продукции, число эшелонов и связанное с ним
размещение запасов.
При выборе варианта размещения распределительного центра применяется следующая последовательность действий:
- изучается конъюнктура рынка; прогнозируется величина материального потока, проходящего через всю логистическую систему;
- составляется прогноз необходимой величины запасов во всей системе, а также на отдельных участках товаропроводящей цепи;
- разрабатывается система товароснабжения;
- проектируется схема распределения материального потока;
- выбирается вариант места расположения распределительного центра по критерию минимума приведенных затрат:
 , (100) , (100)
где  приведенные затраты по варианту; приведенные затраты по варианту;
 годовые эксплуатационные расходы, зависящие от проекта распределительного центра; годовые эксплуатационные расходы, зависящие от проекта распределительного центра;
 годовые транспортные расходы; годовые транспортные расходы;
 капитальные вложения, в строительство распределительного центра; капитальные вложения, в строительство распределительного центра;
 срок окупаемости, лет. срок окупаемости, лет.
На выбор места расположения распределительного центра оказывают влияние два основных фактора: количество потенциальных потребителей, обслуживаемых центром; общая прибыль предприятия (продавца). При этом для выбора варианта размещения распределительного центра выступает величина транспортных расходов, которая может существенно меняться не только от количества распределительных центров, но также от места расположения этих центров на обслуживаемой территории.
Необходимость решения данной задачи возникает при наличии развитой транспортной сети, так как противном случае решение, скорее всего, будет тривиальным. Например, если на территории района есть только две пересекающиеся магистрали, вдоль которых расположены все предполагаемые потребители, то очевидно, что распределительный центр необходимо расположить на пересечении магистралей.
Рассмотрим некоторые алгоритмы оптимальной дислокации распределительных центров[12, 13].
Предположим, что на заданной территориальной зоне (регионе, городе, районе) известны потенциальные потребители продукции фирмы, их месторасположение, объемы спроса в целом и по каждым номенклатурным группам, а также характеристика транспортной сети и маршруты доставки.
Необходимо найти вариант оптимального размещения распределительных центров, обеспечивающий минимум суммарных логистических издержек. При этом критерий оптимизации имеет вид:
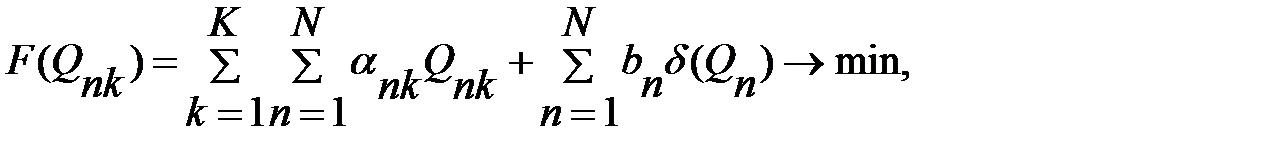
(101)
где 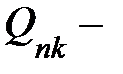 величина годовой поставки величина годовой поставки  му потребителю с му потребителю с  го распределительного центра; го распределительного центра;
 удельные переменные транспортно – складские расходы по доставке продукции от поставщиков удельные переменные транспортно – складские расходы по доставке продукции от поставщиков  му потребителю через му потребителю через 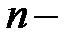 й распределительный центр; й распределительный центр;
 условно – постоянные логистические издержки условно – постоянные логистические издержки  го склада, не зависящие от объема реализации; го склада, не зависящие от объема реализации;
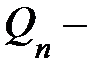 годовой объем реализации продукции с годовой объем реализации продукции с  го распределительного центра; го распределительного центра;  если если   ели ели 
Целевая функция (9.2) дополняется тремя ограничениями:
1) удовлетворение потребителей в складских поставках со всех распределительных центров:
 (102) (102)
где  годовая потребность (спрос) годовая потребность (спрос)  го потребителя; го потребителя;
2) сумма поставок потребителям с распределительного центра должна равняться его объему реализации:
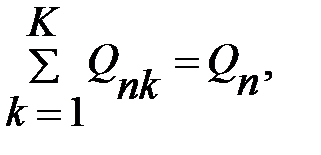 (103) (103)
3) не отрицательность переменных:
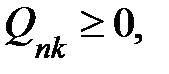 (104) (104)
Для нахождения оптимального плана размещения распределительных центров с использованием сформулированной постановки применяется алгоритм комбинаторного поиска последовательных оценок вариантов [12].
Оптимальная дислокация распределительных центров различного уровня может быть найдена с помощью следующего алгоритма.
Постановка задачи. Имеется  потребителей в некоторой территориальной зоне, заданных координатами ( потребителей в некоторой территориальной зоне, заданных координатами ( ), ),  . Каждый потребитель характеризуется объемом спроса на продукт . Каждый потребитель характеризуется объемом спроса на продукт  , ,  . Требуется определить координаты распределительного центра ( . Требуется определить координаты распределительного центра ( ) так, чтобы сумма расстояний от данных ) так, чтобы сумма расстояний от данных  точек с учетом спроса точек с учетом спроса  до точки с координатами( до точки с координатами( ) была минимальной. В этом случае целевую функцию можно записать следующим образом: ) была минимальной. В этом случае целевую функцию можно записать следующим образом:
 (105) (105)
Таким образом, поставленная задача является классической оптимизационной задачей. То есть необходимо найти координаты распределительного центра ( ) такие которые приводили бы целевую функцию (8.14) к минимуму. Из математики известно, что функция достигает к минимуму в точке, где первое производное этой функции по аргументам равняется нулю. Поэтому возьмем частные производные и полученные выражения приравняем к нулю: ) такие которые приводили бы целевую функцию (8.14) к минимуму. Из математики известно, что функция достигает к минимуму в точке, где первое производное этой функции по аргументам равняется нулю. Поэтому возьмем частные производные и полученные выражения приравняем к нулю:


Решит эту систему уравнений можно найти координаты предполагаемого распределительного центра. Однако решение данной системы уравнений наталкивается серьезные трудности в связи ее нелинейности. Поэтому для поиска минимума целевой функций (105) используется известный итерационный алгоритм:
 ; (106) ; (106)
 , (107) , (107)
где j - номер итерации;
 - потребность i -ого потребителя; - потребность i -ого потребителя;
 - приближенное расстояние от предполагаемого распределительного центра до i -ого населенного пункта, определяемое по формуле: - приближенное расстояние от предполагаемого распределительного центра до i -ого населенного пункта, определяемое по формуле:
 (108) (108)
где  и и  - абсцисса и ордината предполагаемого распределительного центра, полученные в j – 1-ой итерации. - абсцисса и ордината предполагаемого распределительного центра, полученные в j – 1-ой итерации.
Очевидно, что для начала итерационного процесса необходимо знать приближенные координаты предполагаемого распределительного центра ( ), которые находятся по формулам соответственно: ), которые находятся по формулам соответственно:
 (109) (109)
 , (110) , (110)
Процесс итерации продолжается, до тех пор пака не будет выполняться неравенство:
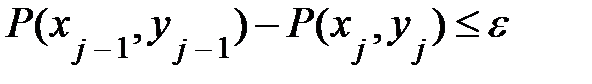 , (111) , (111)
где 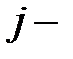 номер итерации; номер итерации;
 малое положительное число (заданная степень точности). малое положительное число (заданная степень точности).
Рассмотрим пример оптимального размещения распределительного центра на заданной территории на основании представленного выше итерационного алгоритма. На логистическом полигоне представлены населенные пункты (таблица 8.2). Необходимо оптимально расположить распределительный центр фирмы при следующих условиях:
1) торгующие организации, расположенные в населенных пунктах, будут снабжаться предполагаемым распределительным центром;
2) планируемая годовая норма потребления товарно-материальных ценностей на одного человека – 3 тонны.
Таблица 8.2
Исходные данные
| Номера
населенных пунктов
| Координаты населенных пунктов, км
| Численность населения,
тыс. чел.

| абсцисса

| ордината
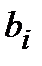
| |
|
|
|
2,243
2,410
1,730
1,110
1,410
1,510
1,810
0,910
1,140
2,020
1,050
0,810
|
Потребность населенного пункта рассчитаем по формуле:
 , (112) , (112)
Пусть точность вычисления составляет  . .
Вычисление координат распределительного центра расположим в таблицах.
Таблица 8.3
Вычисление приближенных координат предполагаемого распределительного центра
| Номера
населенных пунктов
| Координаты населенных пунктов, км
| Потребность
населенного пункта, тыс. т

| 
| 
| абсцисса

| ордината
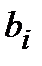
| |
|
|
| 6,73
7,23
5,19
3,33
4,23
4,53
5,43
2,73
3,42
6,06
3,15
2,43
| 868,17
2169,00
2901,21
532,80
1201,32
1852,77
2872,47
1689,87
2941,20
3333,00
185,85
2211,30
| 3869,75
3680,07
3529,20
2027,97
1269,00
3442,80
543,00
2047,50
3108,58
3872,34
1417,50
1965,87
| | Итого
| —
| —
| 54,46
| 22758,96
| 30773,78
|
На основании таблицы 8.3 по формулам (8.18) и (8.19) найдем приближенные координаты распределительного центра:
 км; км;  км. км.
Вычисление координат распределительного центра в первой итерации сведем в таблицу 8.4.
Таблица 8.4
Таблица первой итерации
| №
п/п
| Координаты, км.
| 
| 
| 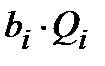
| 
| 
| 
| 
| 
| 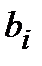
| |
|
|
| 6,73
7,23
5,19
3,33
4,23
4,53
5,43
2,73
3,42
6,06
3,15
2,43
| 868,17
2169,00
2901,21
532,80
1201,32
1852,77
2872,47
1689,87
2941,20
3333,00
185,85
2211,30
| 3869,75
3680,07
3529,20
2027,97
1269,00
3442,80
543,00
2047,50
3108,58
3872,34
1417,50
1965,87
| 289,073
130,056
181,982
261,616
296,972
195,132
478,157
273,202
560,123
151,383
376,898
549,237
| 0,023
0,056
0,029
0,013
0,014
0,023
0,011
0,010
0,006
0,040
0,008
0,004
| 3,003
16,677
15,942
2,037
4,045
9,495
6,007
6,185
5,251
22,017
0,493
4,026
| 13,387
28,296
19,393
7,752
4,273
17,643
1,136
7,494
5,550
25,580
3,761
3,597
| | Итого
| —
| —
| —
| —
| —
| —
| 0,237
| 95,178
| 137,844
|
Примечание: 
На основании полученных результатов по формулам (8.18) и (8.19) рассчитаем координаты распределительного центра в первой итерации:
 км; км;  км. км.
Определим значение целевой функции, которая составляет:
 15538,68377 т. км. 15538,68377 т. км.
Таблица 8.5
Таблица второй итерации
| №
п/п
| Координаты, км
| 
| 
| 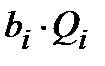
| 
| 
| 
| 
| 
| 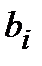
| |
|
|
| 6,73
7,23
5,19
3,33
4,23
4,53
5,43
2,73
3,42
6,06
3,15
2,43
| 868,17
2169,00
2901,21
532,80
1201,32
1852,77
2872,47
1689,87
2941,20
3333,00
185,85
2211,30
| 3869,75
3680,07
3529,20
2027,97
1269,00
3442,80
543,00
2047,50
3108,58
3872,34
1417,50
1965,87
| 272,675
124,881
185,620
243,142
305,186
178,534
498,186
274,985
563,305
159,112
367,008
556,936
| 0,025
0,058
0,028
0,014
0,014
0,025
0,011
0,010
0,006
0,038
0,009
0,004
| 3,184
17,369
15,630
2,191
3,936
10,378
5,766
6,145
5,221
20,948
0,506
3,970
| 14,192
29,469
19,013
8,341
4,158
19,284
1,090
7,446
5,519
24,337
3,862
3,530
| | Итого
| —
| —
| —
| —
| —
| —
| 0,242
| 95,244
| 140,241
|
На основании полученных результатов по формулам (8.18) и (8.19) рассчитаем координаты распределительного центра во второй итерации:
 км; км;  км. км.
Далее необходимо рассчитать целевую функцию:
 15466,72937 т. км. 15466,72937 т. км.
Сравнивая целевые функции, полученные в первой и во второй итерации, приходим к выводу, что имеется тенденция к уменьшению целевой функции от итерации к итерации.
Таблица 8.6
Таблица третьей итерации
| №
п/п
| Координаты, км.
| 
| 
| 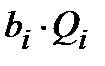
| 
| 
| 
| 
| 
| 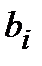
| |
|
|
| 6,73
7,23
5,19
3,33
4,23
4,53
5,43
2,73
3,42
6,06
3,15
2,43
| 868,17
2169,00
2901,21
532,80
1201,32
1852,77
2872,47
1689,87
2941,20
3333,00
185,85
2211,30
| 3869,75
3680,07
3529,20
2027,97
1269,00
3442,80
543,00
2047,50
3108,58
3872,34
1417,50
1965,87
| 264,608
117,161
193,561
235,425
300,217
181,150
498,266
282,641
571,071
167,361
358,761
565,125
| 0,025
0,062
0,027
0,014
0,014
0,025
0,011
0,010
0,006
0,036
0,009
0,004
| 3,281
18,513
14,989
2,263
4,002
10,228
5,764
5,979
4,975
19,915
0,518
3,913
| 14,624
31,410
18,233
8,614
4,227
19,005
1,090
7,244
5,444
23,138
3,951
3,479
| | Итого
| —
| —
| —
| —
| —
| —
| 0,243
| 94,340
| 140,459
|
На основании полученных результатов по формулам (8.18) и (8.19) рассчитаем координаты распределительного центра во второй итерации:
 км; км;  км. км.
Вычислим целевую функцию:
 15454,77581 т. км. 15454,77581 т. км.
Для проверки условии (8.20) найдем разность:
 11,95356. 11,95356.
Так как это разность больше 10, то процесс итерации необходимо продолжить.
Таблица 8.7
Таблица четвертой итерации
| №
п/п
| Координаты, км.
| 
| 
| 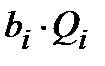
| 
| 
| 
| 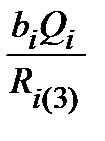
| 
| 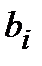
| |
|
|
| 6,73
7,23
5,19
3,33
4,23
4,53
5,43
2,73
3,42
6,06
3,15
2,43
| 868,17
2169,00
2901,21
532,80
1201,32
1852,77
2872,47
1689,87
2941,20
3333,00
185,85
2211,30
| 3869,75
3680,07
3529,20
2027,97
1269,00
3442,80
543,00
2047,50
3108,58
3872,34
1417,50
1965,87
| 259,248
112,020
198,902
230,323
296,917
183,160
498,317
287,805
576,293
172,881
353,245
570,610
| 0,026
0,065
0,026
0,014
0,014
0,025
0,011
0,009
0,006
0,035
0,009
0,004
| 3,354
19,500
14,534
2,240
3,976
10,225
5,819
5,571
5,160
19,250
0,531
3,640
| 14,950
33,085
17,680
8,526
4,200
19,000
1,100
6,750
5,454
22,365
4,050
3,236
| | Итого
| —
| —
| —
| —
| —
| —
| 0,244
| 93,800
| 140,396
|
Рассчитаем координаты распределительного центра в четвертой итерации:
 км; км; 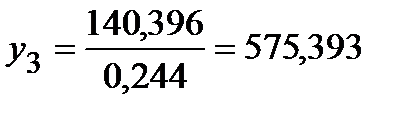 км. км.
Для этих координат необходимо получить целевую функцию:
 15449,04825. 15449,04825.
Вычислим разность:
 5,72756. 5,72756.
Так как это разность меньше заданной точности вычислении (5,72756  ) то минимум целевой функции найдена. Поэтому процесс итерации необходимо прекратить. ) то минимум целевой функции найдена. Поэтому процесс итерации необходимо прекратить.
На основании полученных координат  , ,  определим населенный пункт, где будет либо арендоваться, либо строиться распределительный центр. Таким населенным пунктом является второй населенный пункт, так как вычисленные координаты распределительного центра в третьей итерации ближе подходят к координатам данного населенного пункта. Следовательно, здесь будет размещаться распределительный центр. определим населенный пункт, где будет либо арендоваться, либо строиться распределительный центр. Таким населенным пунктом является второй населенный пункт, так как вычисленные координаты распределительного центра в третьей итерации ближе подходят к координатам данного населенного пункта. Следовательно, здесь будет размещаться распределительный центр.

Шрифт зодчего Шрифт зодчего состоит из прописных (заглавных), строчных букв и цифр...
|

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|
Виды нарушений опорно-двигательного аппарата у детей В общеупотребительном значении нарушение опорно-двигательного аппарата (ОДА) идентифицируется с нарушениями двигательных функций и определенными органическими поражениями (дефектами)...
Особенности массовой коммуникации Развитие средств связи и информации привело к возникновению явления массовой коммуникации...
Тема: Изучение приспособленности организмов к среде обитания Цель:выяснить механизм образования приспособлений к среде обитания и их относительный характер, сделать вывод о том, что приспособленность – результат действия естественного отбора...
|
Понятие метода в психологии. Классификация методов психологии и их характеристика Метод – это путь, способ познания, посредством которого познается предмет науки (С...
ЛЕКАРСТВЕННЫЕ ФОРМЫ ДЛЯ ИНЪЕКЦИЙ К лекарственным формам для инъекций относятся водные, спиртовые и масляные растворы, суспензии, эмульсии, новогаленовые препараты, жидкие органопрепараты и жидкие экстракты, а также порошки и таблетки для имплантации...
Тема 5. Организационная структура управления гостиницей 1. Виды организационно – управленческих структур. 2. Организационно – управленческая структура современного ТГК...
|
|

 , (100)
, (100) приведенные затраты по варианту;
приведенные затраты по варианту; годовые эксплуатационные расходы, зависящие от проекта распределительного центра;
годовые эксплуатационные расходы, зависящие от проекта распределительного центра; годовые транспортные расходы;
годовые транспортные расходы; капитальные вложения, в строительство распределительного центра;
капитальные вложения, в строительство распределительного центра; срок окупаемости, лет.
срок окупаемости, лет.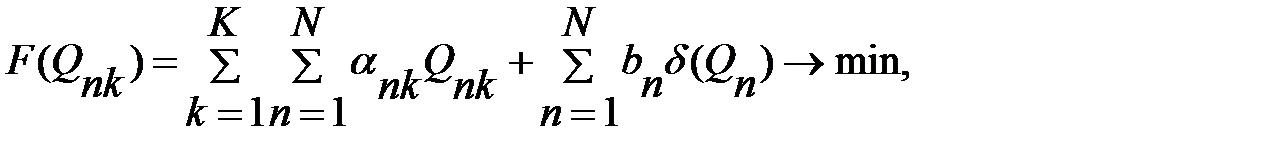
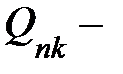 величина годовой поставки
величина годовой поставки  му потребителю с
му потребителю с  го распределительного центра;
го распределительного центра; удельные переменные транспортно – складские расходы по доставке продукции от поставщиков
удельные переменные транспортно – складские расходы по доставке продукции от поставщиков  му потребителю через
му потребителю через 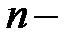 й распределительный центр;
й распределительный центр; условно – постоянные логистические издержки
условно – постоянные логистические издержки  го склада, не зависящие от объема реализации;
го склада, не зависящие от объема реализации;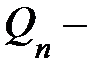 годовой объем реализации продукции с
годовой объем реализации продукции с  го распределительного центра;
го распределительного центра;  если
если 
 ели
ели 
 (102)
(102) годовая потребность (спрос)
годовая потребность (спрос)  го потребителя;
го потребителя;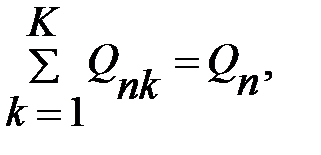 (103)
(103)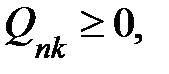 (104)
(104) потребителей в некоторой территориальной зоне, заданных координатами (
потребителей в некоторой территориальной зоне, заданных координатами ( ),
),  . Каждый потребитель характеризуется объемом спроса на продукт
. Каждый потребитель характеризуется объемом спроса на продукт  ,
,  . Требуется определить координаты распределительного центра (
. Требуется определить координаты распределительного центра ( ) так, чтобы сумма расстояний от данных
) так, чтобы сумма расстояний от данных  точек с учетом спроса
точек с учетом спроса  до точки с координатами(
до точки с координатами( ) была минимальной. В этом случае целевую функцию можно записать следующим образом:
) была минимальной. В этом случае целевую функцию можно записать следующим образом: (105)
(105) ) такие которые приводили бы целевую функцию (8.14) к минимуму. Из математики известно, что функция достигает к минимуму в точке, где первое производное этой функции по аргументам равняется нулю. Поэтому возьмем частные производные и полученные выражения приравняем к нулю:
) такие которые приводили бы целевую функцию (8.14) к минимуму. Из математики известно, что функция достигает к минимуму в точке, где первое производное этой функции по аргументам равняется нулю. Поэтому возьмем частные производные и полученные выражения приравняем к нулю:

 ; (106)
; (106) , (107)
, (107) - потребность i -ого потребителя;
- потребность i -ого потребителя; - приближенное расстояние от предполагаемого распределительного центра до i -ого населенного пункта, определяемое по формуле:
- приближенное расстояние от предполагаемого распределительного центра до i -ого населенного пункта, определяемое по формуле: (108)
(108) и
и  - абсцисса и ордината предполагаемого распределительного центра, полученные в j – 1-ой итерации.
- абсцисса и ордината предполагаемого распределительного центра, полученные в j – 1-ой итерации. ), которые находятся по формулам соответственно:
), которые находятся по формулам соответственно: (109)
(109) , (110)
, (110)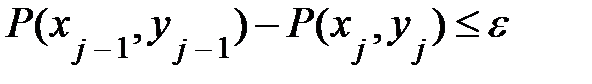 , (111)
, (111)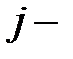 номер итерации;
номер итерации; малое положительное число (заданная степень точности).
малое положительное число (заданная степень точности).

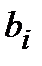
 , (112)
, (112) .
.


 км;
км;  км.
км.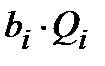





 км;
км;  км.
км. 15538,68377 т. км.
15538,68377 т. км.



 км;
км;  км.
км. 15466,72937 т. км.
15466,72937 т. км.



 км;
км;  км.
км. 15454,77581 т. км.
15454,77581 т. км. 11,95356.
11,95356.


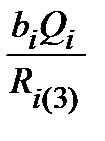
 км;
км; 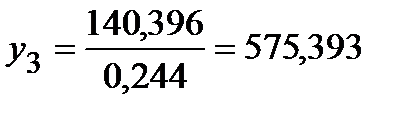 км.
км. 15449,04825.
15449,04825. 5,72756.
5,72756. ) то минимум целевой функции найдена. Поэтому процесс итерации необходимо прекратить.
) то минимум целевой функции найдена. Поэтому процесс итерации необходимо прекратить. ,
,  определим населенный пункт, где будет либо арендоваться, либо строиться распределительный центр. Таким населенным пунктом является второй населенный пункт, так как вычисленные координаты распределительного центра в третьей итерации ближе подходят к координатам данного населенного пункта. Следовательно, здесь будет размещаться распределительный центр.
определим населенный пункт, где будет либо арендоваться, либо строиться распределительный центр. Таким населенным пунктом является второй населенный пункт, так как вычисленные координаты распределительного центра в третьей итерации ближе подходят к координатам данного населенного пункта. Следовательно, здесь будет размещаться распределительный центр.


