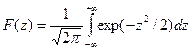Законы распределения непрерывных случайных величин, применяемые в теории надежности1. Экспоненциальное распределение
l - интенсивность отказов.
Этот закон характеризует процессы возникновения и устранения отказов на этапе эксплуатации (l=const) 2. Распределение Вейбулла
q - параметр, определяющий масштаб распределения. Вероятность безотказной работы (ВБР) Средняя наработка до отказа l(t)=f(t)/P(t)=m×tm-1/q при m=1, f(t)=(e-t/q)/q - экспоненциальное распр. при m=2, f(t)=(2/q)exp(-t2/q) – распределение Релея s2=q/2 Характеризует при m>1 старение, износ; при m<1 - переработка 3. Распределение Релея.
4. Гамма-распределение.
k – определяет форму распределения; l0 – масштаб. при k=1 – экспоненциальное распределение; if k – целое, то Г(k)=(k-1)! Характеризует режим переработки 5. Нормальное и усеченное нормальное распределение.
. Условие нормировки Tcp>>s. Отсекаем часть кривой t<0 и вводим нормирующий множитель С.
1. 2. F(-z)=1-F(z). Усеченное нормальное распределение характеризует период старения, износа. Нормальное распределение является предельным, к которому приближаются другие распределения при стремлении к бесконечности числа испытаний.
|
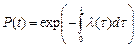; l(t)=f(t)/P(t). При l=const, P(t)=e-tl; f(t)=l×e-tl; 
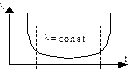При l=const – период нормальной эксплуатации.
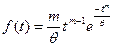, t³0, m>0, q>0. m – параметр, определяющий форму распределения;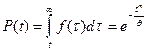
; 
; 
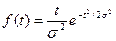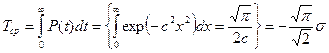;l(t)=t/s2
; 
; 
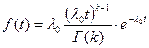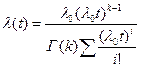; Tcp=k/l0
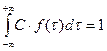Þ 
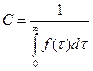
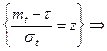
, где 
, где 
