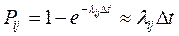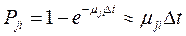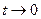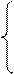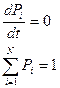Расчет надежности восстанавливаемых систем, основанные на состоянии графа переходов системы.

Случайное событие – это событие, которое может появляться или не появляться в результате данного опыта.

Случайные события, следующие одно за другим в некоторой последовательности, образуют поток случайных событий.

Свойства:

1) Одинарный поток событий – поток, при котором вероятность попадания 2^х событий на один и тот же малый участок времени ∆t пренебрежимо мала.

2) Стационарный поток случайных событий – поток, однородный по времени, т.е. среднее число событий в единицу времени остается постоянным.

3) Поток без последействия – поток, для кот-го для 2^х непрерывающихся временных участков число событий, попадающих на один из них, не зависит от того, сколько событий попало на другой участок.

Отсутствие последействия в потоке означает также, что будущее развитие процесса появляющихся событий не зависит от того, как этот процесс протекал в прошлом.

Простейший поток (Пуассоновский) – обладает всеми 3-мя свойствами.

Случайная величина – величина в результате опыта может принимать то или иное значение, заранее неизвестное.

Случайная функция – функция в результате опыта может принять тот или иной вид, заранее неизвестный.

Если аргументом случайной функции является время, то она называется вероятностным или случайным событием.

Понятие поток событий и процесс взаимосвязаны.

Процесс смены состояния объекта вызывается потоками отказов и потоками восстановлений.

Чтобы охарактеризовать случайный процесс, необходимо указать тип процесса и его численные характеристики.

Марковский процесс – для каждого момента времени вероятность любого состояния в будущем зависит только от ее состояния в настоящий момент времени и не зависит от того, каким образом система пришла в это состояние.

Характеристику процесса удобно представлять в виде графа состояний.

- переходы

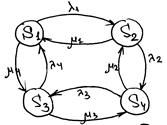
- состояния

S₁ – все работают

S₂ – 1 не работает, 2 работают

S₃ – 2 не работают, 1 работает

S₄ – 1,2 не работают

λ – интенсивность отказов

μ – интенсивность восстановления

 

Вероятности того, что система будет находиться в i-том состоянии:

P₁(t+∆t)=p₁(t)p₁₁(∆t)+p₂(t)p₂₁(∆t)+p₃(t)p₃₁(∆t)

P₂(t+∆t)=p₂(t)p₂₂(∆t)+p₁(t)p₁₂(∆t)+p₄(t)p₄₂(∆t)

…

P_ij(∆t) – вероятность отказа

P_ji(∆t) – вероятность восстановления

 

P₁(t+∆t)=p₁(t)[1-(p₁₂(∆t)+p₁₃(∆t))]+…

при

 

1 – система работоспособна (единственное состояние)

2, 3, 4 – вероятность отказа системы

Р₁ – ВБР системы

В левой части производная по t для вероятности того, что мы определяем.

В правой части столько слагаемых, сколько входит и выходит стрелок («-» если стрелка выходит).

 

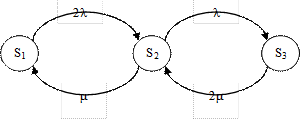
Если λ₁ = λ₂ = λ; μ₁ = μ₂ = μ

Если имеются 2 ремонтные бригады

S₁ – все работают

S₂ – 1 работает, 1 отказал

S₃ – все не работают