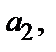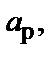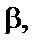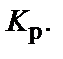Определяется диаметр стержня, высота обмоток и диаметр осевого канала между обмотками. Дополнительно определяется площадь сечения стержня.
Стержень имеет форму ступенчатой фигуры. Диаметр описанной вокруг этой ступенчатой фигуры окружности 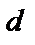 называется диаметром стержня и является первым из основных размеров трансформатора.
называется диаметром стержня и является первым из основных размеров трансформатора.
Вторым основным размером трансформатора является осевой размер 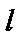 (высота) его обмоток. Обычно обе обмотки трансформатора имеют одинаковую высоту. В случае различия в высоте (это выяснится только при расчете обмоток, что и будет показано в гл. 2) за размер
(высота) его обмоток. Обычно обе обмотки трансформатора имеют одинаковую высоту. В случае различия в высоте (это выяснится только при расчете обмоток, что и будет показано в гл. 2) за размер  принимают их среднее арифметическое значение.
принимают их среднее арифметическое значение.
Третьим основным размером трансформатора является средний диаметр витка двух обмоток или диаметр осевого канала между обмотками 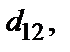 связывающий диаметр стержня с радиальными размерами обмоток
связывающий диаметр стержня с радиальными размерами обмоток 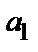 и
и  и осевым каналом между ними
и осевым каналом между ними 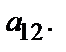
Изображение трансформатора, на котором видны его основные размеры, показано на рис. 4.1.
Диаметр стержня предварительно определить по формуле:
 . (1.10)
. (1.10)
Здесь  – по формуле (1.1);
– по формуле (1.1);  – заданная ширина приведенного канала рассеяния трансформатора (см. формулу 1.11.);
– заданная ширина приведенного канала рассеяния трансформатора (см. формулу 1.11.);  – заданный коэффициент, приближенно равный отношению средней длины витка двух обмоток трансформатора к их высоте, что определяет соотношение между шириной и высотой трансформатора (табл. 1.5);
– заданный коэффициент, приближенно равный отношению средней длины витка двух обмоток трансформатора к их высоте, что определяет соотношение между шириной и высотой трансформатора (табл. 1.5); 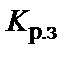 – заданный коэффициент приведения идеального поля рассеяния к реальному (коэффициент Роговского), предварительно принять
– заданный коэффициент приведения идеального поля рассеяния к реальному (коэффициент Роговского), предварительно принять 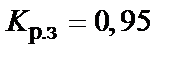 ;
; 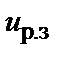 – по формуле (1.8);
– по формуле (1.8); 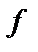 – частота сети (см. задание);
– частота сети (см. задание);  – заданная индукция в стержне (для рулонной электротехнической стали), выбирается предварительно в пределах 1,60–1,65;
– заданная индукция в стержне (для рулонной электротехнической стали), выбирается предварительно в пределах 1,60–1,65; 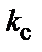 – по формуле (1.9).
– по формуле (1.9).
Таблица 1.5
Коэффициент 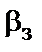
Мощность
трансформатора
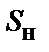 , кВ×А , кВ×А
| Материал обмоток
|
| Медь
| Алюминий
|
| Класс напряжения трансформатора, кВ
|
| 6 и 10
| 35 и 20
| 6 и 10
| 35 и 20
|
Коэффициент 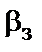
|
| 25−100
| 1,8–2,4
| −
| 1,2–1,6
| −
|
| 160−630
| 1,8–2,4
| 1,8–2,4
| 1,2–1,6
| 1,2–1,5
|
| 1000−6300
| 2,0–2,6
| 1,8–2,4
| 1,3–1,7
| 1,2–1,6
|
| 6300−16000
| −
| 1,7–2,0
| −
| 1,1–1,3
|
| | | | | | | | |
Следует отметить, что данная формула неочевидна, поэтому рекомендуется детально проследить ее вывод в литературе.
Итак, для определения диаметра 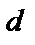 все входящие в формулу (1.10) параметры известны, за исключением заданной ширины приведенного канала рассеяния:
все входящие в формулу (1.10) параметры известны, за исключением заданной ширины приведенного канала рассеяния:
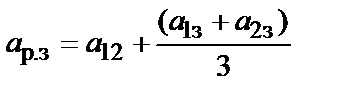 . (1.11)
. (1.11)
Здесь  – по табл. 1.3;
– по табл. 1.3;  – заданный суммарный приведенный радиальный размер (приведенная ширина) обмоток ВН и НН:
– заданный суммарный приведенный радиальный размер (приведенная ширина) обмоток ВН и НН:
 , (1.12)
, (1.12)
где  – коэффициент по табл. 1.6;
– коэффициент по табл. 1.6; 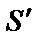 – по формуле (1.1).
– по формуле (1.1).
Таблица 1.6
Коэффициент 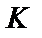
Мощность
трансформатора
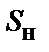 , кВ×А , кВ×А
| Материал обмоток
|
| Медь
| Алюминий
|
| Класс напряжения (обмотки ВН), кВ
|
| 6 и 10
| 35 и 20
| 6 и 10
| 35 и 20
|
Коэффициент 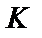
|
| До 250
| 0,63
| 0,65–0,58
| 0,79
| 0,81–0,73
|
| 400–630
| 0,53
| 0,65–0,58
| 0,66
| 0,81–0,73
|
| 1000–6300
| 0,51–0,43
| 0,52–0,48
| 0,61–0,54
| 0,65–0,60
|
| 10000–80000
| –
| 0,48–0,46
| –
| 0,60–0,58
|
| | | | | | | |
Полученный по формуле (1.10) размер диаметра 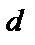 округлить до ближайшего
округлить до ближайшего  по следующей нормализованной шкале в метрах:
по следующей нормализованной шкале в метрах:
0,08; 0,09; 0,1; 0,11; 0,12; 0,125; 0,13; 0,14; 0,15; 0,16; 0,17; 0,18; 0,19; 0,2; 0,21; 0,22; 0,23; 0,24; 0,25; 0,26; 0,27; 0,28; 0,29; 0,3; 0,31; 0,32; 0,33; 0,34; 0,35; 0,36; 0,37; 0,38; 0,39; 0,4; 0,42; 0,45; 0,48; 0,5; 0,53; 0,56; 0,6; 0,63; 0,67; 0,71; 0,75.
Величина  должна быть равна указанной или находиться в указанных в табл. 1.4 пределах. В случае несоответствия необходимо подставить в формулу (1.10) другие числовые значения, пользуясь тем, что часть входящих в нее величин выбрана предварительно и может варьироваться. Таким образом, первый основной размер трансформатора будет определен.
должна быть равна указанной или находиться в указанных в табл. 1.4 пределах. В случае несоответствия необходимо подставить в формулу (1.10) другие числовые значения, пользуясь тем, что часть входящих в нее величин выбрана предварительно и может варьироваться. Таким образом, первый основной размер трансформатора будет определен.
После этого определяется коэффициент  , соответствующий выбранному диаметру
, соответствующий выбранному диаметру 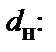
 (1.13)
(1.13)
Значение  должно находиться в пределах, указанных в табл. 1.5. В противном случае следует подставить в формулу (1.10) другие числовые значения и добиться попадания
должно находиться в пределах, указанных в табл. 1.5. В противном случае следует подставить в формулу (1.10) другие числовые значения и добиться попадания  в границы, заданные в табл. 1.5.
в границы, заданные в табл. 1.5.
После этого удобно предварительно определить третий основной размер трансформатора, т. е. заданный средний диаметр канала между обмотками:
 . (1.14)
. (1.14)
Здесь параметр  уже известен точно, параметры
уже известен точно, параметры 
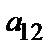 также известны точно как минимальные изоляционные промежутки (рис. 1.1) по табл. 1.2 и 1.3 соответственно, а вот параметр
также известны точно как минимальные изоляционные промежутки (рис. 1.1) по табл. 1.2 и 1.3 соответственно, а вот параметр 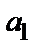 не может быть определен точно до окончательного расчета обмоток (его расчет будет рассмотрен в гл. 2). Поэтому предварительно заданный
не может быть определен точно до окончательного расчета обмоток (его расчет будет рассмотрен в гл. 2). Поэтому предварительно заданный
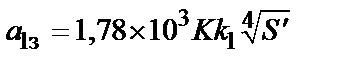 . (1.15)
. (1.15)
Здесь коэффициент 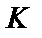 – по табл. 1.6; коэффициент
– по табл. 1.6; коэффициент 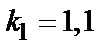 для трансформаторов мощностью до 630 кВ×А включительно, при больших мощностях
для трансформаторов мощностью до 630 кВ×А включительно, при больших мощностях  .
.
Наконец, определяется предварительно второй основной размер трансформатора – заданная высота обмоток:
 , (1.16)
, (1.16)
где  ;
; 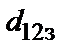 – по формуле (1.14);
– по формуле (1.14);  – по формуле (1.13).
– по формуле (1.13).
После определения основных размеров трансформатора целесообразно определить активное сечение стержня (чистое сечение стали) по формуле:
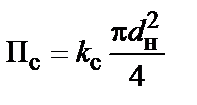 , (1.17)
, (1.17)
где 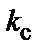 – по формуле (1.9);
– по формуле (1.9);
или по формуле:
 , (1.18)
, (1.18)
где 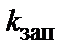 – см. стр. 13–14;
– см. стр. 13–14;  – площадь сечения ступенчатой фигуры стержня (см. прил. 5, 6).
– площадь сечения ступенчатой фигуры стержня (см. прил. 5, 6).
Заметим, что последняя формула будет использоваться и при дальнейших расчетах.
Таким образом, из трех основных размеров трансформатора только диаметр  на настоящий момент определен точно. Остальные размеры
на настоящий момент определен точно. Остальные размеры  и
и  определены только предварительно и будут скорректированы при окончательном расчете. Кроме того, будет скорректирована и часть переменных, входящих в формулу (1.10), а именно будет уточнена при окончательном расчете переменная
определены только предварительно и будут скорректированы при окончательном расчете. Кроме того, будет скорректирована и часть переменных, входящих в формулу (1.10), а именно будет уточнена при окончательном расчете переменная  (об этом уже упоминалось ранее), а также
(об этом уже упоминалось ранее), а также 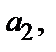
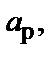
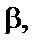

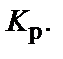

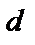 называется диаметром стержня и является первым из основных размеров трансформатора.
называется диаметром стержня и является первым из основных размеров трансформатора.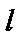 (высота) его обмоток. Обычно обе обмотки трансформатора имеют одинаковую высоту. В случае различия в высоте (это выяснится только при расчете обмоток, что и будет показано в гл. 2) за размер
(высота) его обмоток. Обычно обе обмотки трансформатора имеют одинаковую высоту. В случае различия в высоте (это выяснится только при расчете обмоток, что и будет показано в гл. 2) за размер  принимают их среднее арифметическое значение.
принимают их среднее арифметическое значение.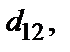 связывающий диаметр стержня с радиальными размерами обмоток
связывающий диаметр стержня с радиальными размерами обмоток 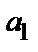 и
и  и осевым каналом между ними
и осевым каналом между ними 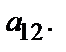
 . (1.10)
. (1.10) – по формуле (1.1);
– по формуле (1.1);  – заданная ширина приведенного канала рассеяния трансформатора (см. формулу 1.11.);
– заданная ширина приведенного канала рассеяния трансформатора (см. формулу 1.11.);  – заданный коэффициент, приближенно равный отношению средней длины витка двух обмоток трансформатора к их высоте, что определяет соотношение между шириной и высотой трансформатора (табл. 1.5);
– заданный коэффициент, приближенно равный отношению средней длины витка двух обмоток трансформатора к их высоте, что определяет соотношение между шириной и высотой трансформатора (табл. 1.5); 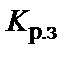 – заданный коэффициент приведения идеального поля рассеяния к реальному (коэффициент Роговского), предварительно принять
– заданный коэффициент приведения идеального поля рассеяния к реальному (коэффициент Роговского), предварительно принять 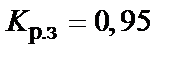 ;
; 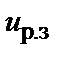 – по формуле (1.8);
– по формуле (1.8); 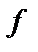 – частота сети (см. задание);
– частота сети (см. задание);  – заданная индукция в стержне (для рулонной электротехнической стали), выбирается предварительно в пределах 1,60–1,65;
– заданная индукция в стержне (для рулонной электротехнической стали), выбирается предварительно в пределах 1,60–1,65; 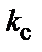 – по формуле (1.9).
– по формуле (1.9).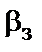
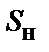 , кВ×А
, кВ×А
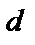 все входящие в формулу (1.10) параметры известны, за исключением заданной ширины приведенного канала рассеяния:
все входящие в формулу (1.10) параметры известны, за исключением заданной ширины приведенного канала рассеяния: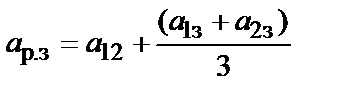 . (1.11)
. (1.11) – по табл. 1.3;
– по табл. 1.3;  – заданный суммарный приведенный радиальный размер (приведенная ширина) обмоток ВН и НН:
– заданный суммарный приведенный радиальный размер (приведенная ширина) обмоток ВН и НН: , (1.12)
, (1.12) – коэффициент по табл. 1.6;
– коэффициент по табл. 1.6; 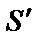 – по формуле (1.1).
– по формуле (1.1).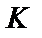
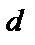 округлить до ближайшего
округлить до ближайшего  по следующей нормализованной шкале в метрах:
по следующей нормализованной шкале в метрах: , соответствующий выбранному диаметру
, соответствующий выбранному диаметру 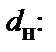
 (1.13)
(1.13) . (1.14)
. (1.14) уже известен точно, параметры
уже известен точно, параметры 
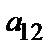 также известны точно как минимальные изоляционные промежутки (рис. 1.1) по табл. 1.2 и 1.3 соответственно, а вот параметр
также известны точно как минимальные изоляционные промежутки (рис. 1.1) по табл. 1.2 и 1.3 соответственно, а вот параметр 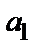 не может быть определен точно до окончательного расчета обмоток (его расчет будет рассмотрен в гл. 2). Поэтому предварительно заданный
не может быть определен точно до окончательного расчета обмоток (его расчет будет рассмотрен в гл. 2). Поэтому предварительно заданный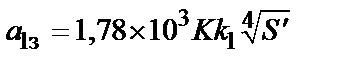 . (1.15)
. (1.15)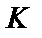 – по табл. 1.6; коэффициент
– по табл. 1.6; коэффициент 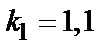 для трансформаторов мощностью до 630 кВ×А включительно, при больших мощностях
для трансформаторов мощностью до 630 кВ×А включительно, при больших мощностях  .
. , (1.16)
, (1.16) ;
; 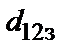 – по формуле (1.14);
– по формуле (1.14); 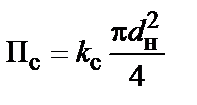 , (1.17)
, (1.17)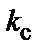 – по формуле (1.9);
– по формуле (1.9); , (1.18)
, (1.18)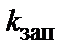 – см. стр. 13–14;
– см. стр. 13–14;  – площадь сечения ступенчатой фигуры стержня (см. прил. 5, 6).
– площадь сечения ступенчатой фигуры стержня (см. прил. 5, 6). на настоящий момент определен точно. Остальные размеры
на настоящий момент определен точно. Остальные размеры  и
и  определены только предварительно и будут скорректированы при окончательном расчете. Кроме того, будет скорректирована и часть переменных, входящих в формулу (1.10), а именно будет уточнена при окончательном расчете переменная
определены только предварительно и будут скорректированы при окончательном расчете. Кроме того, будет скорректирована и часть переменных, входящих в формулу (1.10), а именно будет уточнена при окончательном расчете переменная  (об этом уже упоминалось ранее), а также
(об этом уже упоминалось ранее), а также