Капиллярные явления. Формула Жюрена
Капиллярные явления наблюдаются, когда жидкость проникает в трубки с очень узкими каналами (капилляры, капиллярно-пористые тела), у которых расстояние между стенками соизмеримо с радиусом кривизны поверхности жидкости. Кривизна возникает в результате взаимодействия жидкости со стенками сосуда (адгезия, смачивание). Специфика поведения жидкости в капилляре зависит от того, смачивает или не смачивает жидкость его стенки, точнее, от значения краевого угла смачивания. Рассмотрим положение уровней жидкости в двух капиллярах, один из которых имеет лиофильную поверхность и поэтому стенки его смачиваются, у другого внутренняя поверхность лиофобизирована и не смачивается (рис.30). В первом капилляре (см. рис.30, а)поверхность жидкости имеет отрицательную кривизну, поэтому дополнительное давление Лапласа (давление направлено к центру кривизны) поднимает её в капилляре. Кривизна поверхности жидкости во втором капилляре (см. рис.30, б) положительна, дополнительное давление направлено внутрь жидкости, в результате жидкость в капилляре опускается (отрицательное капиллярное поднятие). При равновесии лапласовское давление равно гидростатическому давлению столба жидкости высотой H:
где r – плотность жидкости; r0 – плотность газовой фазы; g – ускорение свободного падения; r – радиус мениска.
Рис.30. Капиллярное поднятие жидкости: a – cos q > 0: б – cos q < 0: в – связь радиуса кривизны мениска r с радиусом капилляра r0.
Чтобы высоту капиллярного поднятия связать с характеристикой смачивания, радиус мениска необходимо выразить через угол смачивания q и радиус капилляра r 0. На рис.30, в показан (в увеличенном виде) мениск жидкости в капилляре. Видно, что r 0 = r´;cos q, тогда высоту капиллярного поднятия можно представить в виде формулы Жюрена:
При отсутствии смачивания q > 90°, cos q < 0, уровень жидкости в капилляре опускается на величину H. При полном смачивании q = 0, cos q = 1, в этом случае радиус мениска равен радиусу капилляра. Краевой угол для воды и низших углеводородов на стенке стеклянного капилляра мал. Для большинства других жидкостей он меньше 10°. Расчет по уравнению (XII.4) показывает, что относительная погрешность, обусловленная приравниванием этого угла в стеклянном капилляре нулю, не превышает 1,5%. Измерение высоты капиллярного поднятия лежит в основе одного из наиболее точных методов определения поверхностного натяжения жидкостей. Капиллярным поднятием жидкостей объясняется ряд известных явлений и процессов: пропитка бумаги и тканей обусловлена капиллярным поднятием жидкости в порах; водонепроницаемость тканей обеспечивается их гидрофобностью и как следствие – отрицательным капиллярным поднятием; подъем воды из почвы по стволам деревьевпроисходит благодаря волокнистому строению древесины и т. д.
|

 (XII.3)
(XII.3)
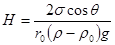 (XII.4)
(XII.4)


