Двухкомпонентные системы
Конденсированные системы Системы без твердой фазы
Неизоморфные конденсир. Изоморф. с ограниченной системы системы с неогра- к.с. (твердые растворимостью ниченной растворимостью р-ры) в тв.состоянии компонентов в жидком и взаимной нерастворимостью в тв. состоянии
4. Равновесие в системах без твердой фазы. К системам без твердой фазы относятся системы жидкость-жидкость, жидкость-пар. Они могут быть одной-, двух- и многокомпонентными. Если система состоит из I компонента, она представляет собой чистую жидкость, находящуюся в равновесии со своим паром. Двухкомпонентные системы без твердой фазы представляют смеси двух жидкостей. Условия фазовых равновесий смесей жидкостей зависят от их взаимной растворимости. При смешивании жидкостей возможны три варианта их растворимости. 1) Неограниченная взаимная растворимость 2) Частичная взаимная растворимость 3) Полная нерастворимость
4.1. Система жидкостей с частичной взаимной растворимостью. При смешивании двух жидкостей с ограниченной растворимостью каждая из них растворяется в другой до определенного предела. Образуются два слоя различного состава. Они представляют собой насыщенные при данной температуре растворы одной жидкости в другой. Обычно с повышением температуры взаимная растворимость жидкостей возрастает. При определенной температуре обе смеси по составу оказываются одинаковыми. Граница между ними исчезает. Жидкости становятся полностью растворимыми. Температура, выше которой достигается полная растворимость жидкостей, называется верхней критической температурой растворения. Если же полная растворимость жидкостей достигается ниже какой-то температуры, то это нижняя критическая температура растворения.
Рис. 1.11 Взаимная раствори- Рис.1.12 Взаимная раствори- мость фенола и воды. мость никотина и воды.
На диаграмме состояния такой системы фенол-вода, левая часть кривой выражает растворимость фенола в воде, правая- растворимость воды в феноле. Система имеет верхнюю критическую точку при 68,3° С. Поле диаграммы внутри кривой характеризует смеси такого состава, которые при температуре ниже 68,3°С разделяются на два слоя. Поле диаграммы снаружи кривой характеризует такие системы, которые при любой температуре могут существовать не расслаиваясь. Часто критические точки оказываются либо выше точки кипения, либо ниже точки отвердевания одной из жидкости, поэтому многие системы жидкостей с частичной взаимной растворимостью при обычном давлении не имеют ни одной критической точки или только одну из них. Вместе с тем существуют системы с обеими критическими точками (никотин- вода).
4.2. Системы жидкостей с неограниченной взаимной растворимостью. 1) Закон Рауля. Идеальные и неидеальные растворы. При полной взаимной растворимости жидкости образуют однородный раствор, находящийся в равновесии с парами жидкости над ним. В идеальном случае давление пара растворителя над раствором ниже, чем над чистым растворителем. Растворенное вещество занимает часть объема раствора, понижает концентрацию молекул растворителя, и соответственно этому уменьшается число их переходящих в пар.
о о о о о о о ох о ох о ох о
растворитель раствор
Рауль в 1886 году установил, что относительное понижение давления пара растворителя над раствором равно мольной доле растворенного вещества.
р° n° + n
р° - давление пара над чистым растворителем, р - давление пара над раствором, n - число молей растворенного вещества, n° - число молей растворителя, р° - р - понижение давления пара растворителя над раствором по сравнению с чистым растворителем, р° - р - относительное понижение давления пара растворителя над раство- р° ром или депрессия раствора. Закон Рауля может быть сформулирован не только по отношению к растворенному веществу, но и применительно к мольной доле растворителя. Для этого уравнение можно преобразовать, вычтя обе части его из единицы:
р° n° + n p° n° + n n° + n Обозначив мольную долю растворителя через N° можно записать: p = р°N° Таким образом, парциальное давление пара каждого компонента над раствором равно произведению мольной доли его в растворе на давление пара, которое он имеет в чистом виде. В растворах испарение каждой из жидкостей происходит независимо от присутствия другой. Общее давление пара над раствором жидкости равно сумме парциальных давлений.
Р общ. = Ра + Рв Р = Ра° х Nа + Рв° х Nв
Эту зависимость можно представить графически.
pобщ = pa+pв pa° pa = pa° Na pв°
pa = pa°Nв
А состав В
Рис. 1.13. Зависимость парциальных и общего давления от состава раствора (идеальный раствор) при t =const
Точка Ра° отвечает давлению пара над чистым компонентом А, а точка Рв° - давлению над чистым компонентом В. Прямая Ра° В выражает зависимость парциального давления пара компонента А от состава, прямая Рв° А - зависимость парциального давления пара компонента В от состава. Общее давление Робщ равное, согласно закону Дальтона, сумме парциальных давлений, выражается прямой Ра° + Рв°. Растворы подчиняются закону Рауля, если силы взаимодействия между частицами разных веществ (А-В) равны силам, действующим между частицами одного и того же вещества (А-А и В-В). При этом смешивание компонентов не сопровождается ни поглощением, ни выделением теплоты или изменением объема.
DV = 0, DH = 0
Однако чаще всего реальные растворы жидкостей проявляют положительные и отрицательные отклонения от закона Рауля. Положительные отклонения можно объяснить меньшими силами взаимодействия между молекулами разного типа (А-В), чем между молекулами одного и того же вещества (А-А и В-В).
Рис. 1.14. Зависимость парциального и общего давления от состава раствора (положительное отклонение от закона Рауля) при t= const.
Примеры: ацетон - сероуглерод, этанол - этиловый эфир.
Отрицательные отклонения от закона Рауля характерны для растворов: вода – хлористый водород, вода – серная кислота. Для данных растворов наблюдается уменьшение давления пара по сравнению с идеальными растворами. Отрицательные отклонения обуславливаются большими силами притяжения между молекулами разных типов (взаимодействие А-В больше, чем А-А и В-В). Отрицательные отклонения наблюдаются у растворов склонных к сольватации, в частности к гидротации. Образование растворов такого типа, как правило, сопровождается уменьшением объема и выделением теплоты, т.е. DV < 0, DH < 0.
Рис.1.15. Зависимость парциальных и общего давления от состава раствора (отрицательное отклонение от закона Рауля) при t=const.
4.3. Состав пара растворов. Зависимость состава пара от состава раствора и общего давления характеризуется двумя законами, открытыми Д.П.Коноваловым (1881). Первый закон Коновалова характеризует соотношения между составами равновесных жидкостей и пара и влияния того или другого из компонентов на общее давление пара. А) Повышение относительного содержания данного компонента в жидкой фазе всегда вызывает увеличение относительного содержания его в парах. В) В двойной системе - пар, по сравнению с находящейся с ним в равновесии жидкостью, относительно богаче тем из компонентов, прибавление которого к системе повышает общее давление пара, т.е. понижает температуру кипения смеси при данном давлении. Второй закон Коновалова относится к азеотропным растворам (нераздельно кипящим или постоянно кипящим раствором). Он устанавливает, что: точки максимума и минимума на кривой общего давления пара отвечают растворам, состав которых одинаков с составом равновесного с ним пара.
4.4. Диаграмма состояния. Температура кипения растворов. При рассмотрении температуры кипения нужно сопоставлять растворы, находящиеся не при одинаковой температуре, а при одинаковом Р. Та из двух сравниваемых жидкостей, которая обладает большим давлением пара при одинаковой температуре, обладает более низкой температурой кипения. На диаграммах представляющих зависимость температуры кипения от состава, обычно принято строить две кривые, одна из которых связывает эти температуры с составом жидкой фазы, а другая - с составом пара. Нижняя кривая относится к составам жидкости (кривая жидкости), а верхняя – к составам пара (кривая пара). Поле диаграммы, расположенной ниже кривой жидкости, представляет состояние растворов различного состава при температурах ниже температур их кипения (поле жидкости). Поле диаграммы, расположенное выше кривой пара, представляет состояние пара различного состава при температурах выше температур конденсации его в жидкость (поле пара). Область между кривыми жидкости и пара отвечает гетерогенным системам, состоящим из равновесных между собой жидкого раствора и пара. Подобный метод сочетания диаграмм применяется и при выражении зависимости давления насыщенного пара от состава жидкости и от состава пара при заданной постоянной температуре. В этом случае состоянию жидкого раствора отвечает поле диаграммы, расположенное над кривой жидкости, состоянию пара поле под кривой пара, а область между кривыми жидкости и пара представляет гетерогенные системы. Системы, обладающие максимумом на кривых давления пара, имеют минимум на кривых температур кипения, и наоборот. Точки максимум и минимум отвечают раствором, состав которых одинаков с составом равновесного с ним пара. Рассмотрим три основные типа таких диаграмм. Буквой В обозначим компонент, обладающий более низкой температурой кипения.
Рис.1.16. Диаграммы состав-давление пара и состав-температура кипения для различных типов систем.
4.5. Перегонка растворов. Различают прямую перегонку и дробную (перегонку с последующей конденсацией пара).
Прямая перегонка заключается в нагреве раствора до температуры кипения и порционном отборе пара.
Рис. 1.17 Прямая перегонка раствора.
Более полное разделение компонентов достигается при конденсации пара. Рассмотрим сначала раствор, не образующий азеотроп.
n1
ж2 tкипВ
А х0 y0=x1 y1=x2 B
Рис.1.18. Дробная перегонка растворов.
Точка Ж0 представляет собой исходный раствор состава х0, точка n0 - равновесный пар состава у0. Конденсация этого пара приводит к жидкому раствору состава у0 = х1 (точка ж1). Испарим этот раствор. Образуется пар (т. n1) состава у1. Конденсация этого пара дает жидкость (т. ж2) состава у1=х2 и т.д. Повторяя достаточное число раз этот процесс, можно прийти сколько угодно близко к точке температуры кипения В, т.е. к чистому второму компоненту при температуре его кипения. При каждом акте испарения жидкость обедняется компонентом В и поэтому кипит при более высокой температуре. Состояние этой жидкости выражается точкой I. Проводя с этой жидкостью такую же последовательность процессов испарение - конденсация, можно снова получить в последнем конденсате чистый компонент В, а сама жидкость при этом сместиться из точки I в точку 2. Таким образом, жидкость будет все время приближаться по составу к чистому, менее летучему компоненту А при температуре его кипения. В результате исходный раствор разделяется на чистые компоненты. Этот процесс разделения жидких растворов на компоненты называется дробной перегонкой или ректификацией. В технике процесс ректификации проводится в специальных ректификационных колоннах, разделенных по высоте горизонтальными перегородками - «тарелками». Каждый отдельный акт конденсация - испарение происходит на отдельной тарелке. В лабораторных условиях высокая эффективность процесса разделения достигается применением дефлегматоров.
Рис. 1.19. Схема лабораторного прибора для перегонки.
Рассмотрим теперь дробную перегонку в растворе, образующем азеотроп. Пусть это будет азеотроп с минимумом на кривой зависимости температуры кипения от состава.
А х0 y0=х1 у1=х2 хАз В
Рис. 1.21. Дробная перегонка раствора, образующего азеотроп (расчет по компоненту В).
Таким образом, для любого исходного раствора, для которого х0 < хаз в результате дробной перегонки получают чистый компонент А при температуре его кипения и азеотроп при Таз. Если исходный раствор имеет состав х0 > хаз, то перегонка приводит к чистому компоненту В и азеотропу при Таз. Если бы раствор имел максимум на кривой Ткип. = f(х), то при х0 < хаз отгоняемый и затем конденсируемый пар привел бы к чистому компоненту А, а жидкость постепенно обогащаясь компонентом В, пришла бы к азеотропу. При х0 >хаз отгоняемый и конденсируемый пар дал бы чистый компонент В, а жидкость пришла бы к азеотропу. Итак, для растворов дающих азеотропы, полное разделение на компоненты методом дробной перегонки невозможно ни при каком числе тарелок. Азеотропные растворы поэтому называются так же нераздельно кипящими смесями.
4.6. Правило рычага. При равновесии жидкость-пар в двойной системе необходимо определить количественное соотношение между жидкостью и паром при различных температурах. Для этих целей используют обычно правило рычага. Точка, отвечающая составу гетерогенной двойной системы располагается на прямой, соединяющей точки, представляющие сосуществующие фазы. При этом отрезки, отсекаемые на прямой этой точкой обратно пропорциональны количествам каждой из фаз.
A xж х0 хn B
4.7. Закон распределения.
Если в систему, состоящую из двух взаимонерастворимых жидкостей, ввести третье вещество, растворимое в обеих жидкостях, то оно распределяется между ними. Проводя экспериментальное и теоретическое изучение этого явления, Нернст в 1890 году выявил закономерность, названную законом распределения: при постоянной температуре отношение концентраций вещества (третьего компонента), растворенного в двух равновесных фазах, постоянно. Например, если в смесь бензола с водой вводить различные количества йода (m1, m2, m3 и т.д.), то каждый раз устанавливаются такие равновесные концентрации йода в водном (С1В, С2В, С3В) и бензольном (С1Б, С2Б, С3Б) слоях, что их отношение остается постоянным.
где К – коэффициент распределения.
В такой форме закон распределения соблюдается лишь при идеальных и бесконечно разбавленных растворов. Поскольку при растворении обычно происходят значительные изменения в строении вещества (диссоциация, ассоциация, сольватация и т.п.), закон распределения видоизменяется. Наиболее точная форма закона распределения предложена Н.А.Шиловым и имеет вид
где n - постоянная, зависящая от температур и природы всех компонентов системы. Если распределяющееся вещество диссоциирует, причем степень диссоциации его в первом растворителе равна a1 , а во втором - a2 то закон распределения принимает вид
4.8. Экстракция. Экстракция – способ извлечения веществ из сложных систем (жидких, твердых или смешанных), обработкой их селективным (избирательным) растворителем, называемым экстрагентом. Чаще всего экстрагент не растворяется в обрабатываемой системе, а является отдельной фазой. В результате экстракции образуются: Экстракт – раствор извлеченных компонентов в экстрагенте, и рафинат – обработанная смесь, обедненная извлекаемыми компонентами. Весь процесс экстракции ведут в спец. аппаратах - экстракторах, различающихся как по конструкции, так и по принципу действия. Принципиальная схема процесса экстракции имеет вид:
(исходная смесь) экстрагент
Рассмотрим применение закона распределения для расчета материального баланса процесса экстракции. Пусть экстракции подвергается исходный раствор объемом V0, содержащий g0 кг экстрагируемого вещества. После введения в него экстрагента объемом Vэ, согласно закону распределения, часть этого вещества перейдет из исходного раствора в экстрагент. Пусть в результате такого перехода образовался рафинат, содержащий g1 кг растворенного вещества, и экстракт, содержащий g0 - g1 кг вещества. Тогда концентрация этого вещества составит: В рафинате - С1 = g1 / V0 M В экстракте - С2 = (g0 – g1) / Vэ М
где М - молярная масса экстрагируемого вещества. Из закона распределения следует выражение
Преобразование которого дает:
Это выражение можно использовать для расчета одноступенчатого процесса экстракции. Т.е. когда исходный раствор обрабатывают экстрагентом лишь один раз. При такой экстракции в рафинате остается довольно много неизвлеченного вещества. Поэтому процесс экстракции повторяют несколько раз, беря каждый раз один и тот же объем свежего экстрагента. Такая экстракция называется многоступенчатой. Уравнение для расчета материального баланса многоступенчатой экстракции имеет вид
Где n - число самостоятельных стадий (ступеней) экстракции.
На практике для повышения эффективности использования экстрагента, кроме применения многоступенчатой экстракции, стремятся проводить процесс при условиях, предупреждающих такие побочные явления, как диссоциация и др. Для этого процесс ведут при пониженной температуре или в присутствии веществ, смещающих равновесие в сторону экстрагируемого вещества.
5. Трехкомпонентные системы.
5.1. Применение правила фаз к трехкомпонентным системам. Для трехкомпонентной системы, на равновесие которой влияют только температура, давление и концентрация компонентов правило фаз Гиббса выражается соотношением С = 5 - Ф Отсюда следует, что в 3-х-компонентной системе одновременно могут находиться в равновесии не более пяти фаз, а максимальная вариантность равна 4 (Ф=1, С=4). К параметрам состояния 3-х-компонентной системы относятся температура, давление и концентрация двух компонентов, поэтому полная диаграмма состояния такой системы должна быть четырехмерной. В связи с этим 3-х-компонентные системы рассматривают при Р=const и строят трехмерную пространственную диаграмму в виде прямой трехгранной призмы, основанием которой служит равносторонний треугольник состава, а по высоте откладывается температура. При Т=const или Р=const С усл. = 4 – Ф А при Т=const и Р=const С усл = 3 - Ф
Изучение равновесий в трехкомпонентной системе еще более упрощается при t=const и P=const, т.к. при этом можно использовать плоскую диаграмму состояния, являющуюся сечением призмы параллельным основанию (диаграмма состава).
5.2. Взаимная растворимость трех жидкостей. Состав 3-х-компонентной системы изображается на диаграмме представляющий правильный треугольник. Вершины равностороннего треугольника соответствуют чистым веществам А, В и С. На сторонах, соединяющих вершины откладываются составы 2-х-компонентной системы, образованных веществами, находящимися в прилегающих вершинах треугольника. Процентное содержание каждого из компонентов в системе тем больше, чем ближе расположена данная точка к соответствующей вершине. Существуют два метода определения состава 3-х-компонентной системы. В методе, предложенном Гиббсом, за 100 % (или 1) принимается высота правильного треугольника. Метод основан на том, что сумма длин перпендикуляров, опущенных из любой точки внутри треугольника на его стороны, есть величина постоянная и равна высоте этого треугольника. Процентное содержание каждого компонента определяется расстоянием от точки Р, отражающей состав системы, до стороны треугольника, противолежащей вершине, соответствующей чистому компоненту. B
c P a
A в C
Рис. 1.22. Треугольник для изображения состава тройных смесей. (метод Гиббса)
Отрезок РА соответствует % содержанию компонента А, отрезок РВ - % содержанию компонента В, РС - компоненту С. По методу Розебума за 100 % (или 1) принимается длина стороны правильного треугольника. Сумма отрезков, проведенных параллельно сторонам треугольника из точки Р, отражающей состав системы (Ра + Рв +Рc), равна стороне треугольника; содержание компонента А - длина отрезков Ра=вС=в¢В=ас/=Рс/, содержание компонента В - длина отрезков Рв=а¢в=Ас=с¢С содержание компонента С - длина отрезков Рс=Аа¢=св¢=Ва Оба метода приводят к одинаковым результатам. B A в’ P
A a’ в C
Рис.1.23. Треугольник для изображения тройных смесей (метод Розебума)
[1] Все сказанное выше относительно испарения действительно и для процесса возгонки (сублимации). [2] Напомним, что фазами называются однородные (гомогенные) части системы, отделенные от остальных частей поверхностями раздела. Фаза имеет во всех точках одинаковый состав и свойства. Каждая фаза характеризуется своим уравнением состояния. [3] Возможности прямого измерения парциальных давлений отсутствуют. Для идеальных газовых смесей, основываясь на законе Дальтона, пишем: Pi где P – полное давление; Pi – парциальное давление и x'i – мольная доля компонента в газовой смеси. Парциальное давление есть, в сущности, мера мольной доли компонента x'i, условно пересчитанной на давление для идеальных газовых смесей. [4] Греческое слово «эбуллиоскопия» означает «наблюдение кипения». [5] Изобарные диаграммы температура кипения - состав имеют обратный вид: максимуму общего давления соответствует минимум температуры кипения и наоборот. [6] При значительных давлениях наблюдается отклонение от уравнения (VI, 1). [7] Если газ находится при температуре выше критической, то применение уравнения Рауля – Генри, строго говоря, невозможно. Однако, используя уравнение Клапейрона - Клаузиуса, условно экстраполируют [8] Уменьшение растворимости в присутствии солей называется высаливанием. Оно наблюдается не только для газов, но и вообще для неэлектролитов. [9] Коллоидная химия – одна из немногих наук, название которой не соответствует содержанию (греч. kolla – клей). Это название было принято раньше, чем коллоидная химия сформировалась в самостоятельную науку. В некоторых странах она переименована в «Поверхностные явления», «Поверхностные явления и коллоиды», «Физическую химию поверхностей» и др.
[А.Р.1]
|





 Без хим.взаимодействия с хим.взаимодействием
Без хим.взаимодействия с хим.взаимодействием








 о о о о о о о о о о о о о о
о о о о о о о о о о о о о о
 о о о о о о о о ох о ох о
о о о о о о о о ох о ох о

 р° - р = n
р° - р = n



 I - р° - р = I - n => p = n° или p = p° n°
I - р° - р = I - n => p = n° или p = p° n° p
p








 tкипА
tкипА 2 ж0 n0
2 ж0 n0
 ж1
ж1







 2 - конденсатор
2 - конденсатор






 1 3 - сборник
1 3 - сборник








 4
4

 3
3

 t°кипА
t°кипА 2 n0
2 n0 1 ж0
1 ж0 

 n1 t°кипВ
n1 t°кипВ ж1
ж1 






 кол – во жидкости = а
кол – во жидкости = а


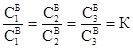










 А С + В
А С + В


 рафинат экстракт
рафинат экстракт






 c c’
c c’
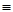 P
P  x'i
x'i до температур выше критической.
до температур выше критической.


