Средняя квадратичная скорость молекул — среднее квадратическое значение модулей скоростей всех молекул рассматриваемого количества газа
В Формуле мы использовали:
16.Термодинамические параметры термодинамические параметры — физические величины, характеризующие состояние термодинамической системы: температура, давление, удельный объём, намагниченность, электрическая поляризация и др. Различают экстенсивные параметры состояния, пропорциональные массе системы:
и интенсивные параметры состояния, не зависящие от массы системы:
Не все параметры состояния независимы, так что равновесное состояние системы можно однозначно определить, установив значения ограниченного числа параметров состояния. ЭНЕРГИЯ ГИББСА это величина, показывающая изменение энергии в ходе химической реакции и дающая таким образом ответ на вопрос о принципиальной возможности протекания химической реакции; это термодинамический потенциал следующего вида:
Энтропия (от греч. entropia — поворот, превращение), понятие, впервые введённое в термодинамике для определения меры необратимого рассеяния энергии.
Энтальпия(Энтальпия (от греч. enthálpo — нагреваю) (теплосодержание, тепловая функция Гиббса), потенциал термодинамический, характеризующий состояние термодинамической системы при выборе в качестве основных независимых переменных энтропии S и давления р. Обозначается H)
Свобо́дная эне́ргия Гельмго́льца (или просто свобо́дная эне́ргия) — термодинамический потенциал, убыль которого в квазистатическом изотермическом процессе равна работе, совершённой системой над внешними телами. Свободная энергия Гельмгольца для системы с постоянным числом частиц определяется так:
17. Внутренняя энергия Вну́тренняя эне́ргия тела (обозначается как E или U) — это сумма энергий молекулярных взаимодействий и тепловых движений молекулы. Внутренняя энергия является однозначной функцией состояния системы. Это означает, что всякий раз, когда система оказывается в данном состоянии, её внутренняя энергия принимает присущее этому состоянию значение, независимо от предыстории системы. Следовательно, изменение внутренней энергии при переходе из одного состояния в другое будет всегда равно разности между ее значениями в конечном и начальном состояниях, независимо от пути, по которому совершался переход. Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:
где
Эта формула является математическим выражением первого начала термодинамики. В каждом теле, в каждом веществе в скрытом виде заключена внутренняя энергия, которая складывается из энергии движения и взаимодействия атомов, молекул, ядер и других частиц, внутриядерную и другие виды энергии, кроме кинетической энергии движения системы, и потенциальной энергии ее положения. Абсолютную величину внутренней энергии определить невозможно. Она представляет собой способность системы к совершению работы или передаче теплоты. где U 2 и U 1- внутренняя энергия системы в конечном и начальном состояниях. Если Δ U > 0–внутренняя энергия системы возрастает, если Δ U < 0– внутренняя энергия системы убывает. U – термодинамическая функция состояния, так как ее количество не будет зависеть от пути и способа перехода системы, а будет определяться лишь разностью в этих состояниях. При переходе из одного состояния в другое система может обмениваться с окружающей средой веществом или энергией в форме теплоты и работы.
18. СТЕПЕНЕЙ СВОБОДЫ ЧИСЛО в механике - число не зависимых между собой возможных перемещений механич. системы. С. с. ч. зависит от числа материальных точек, образующих систему, и от числа и характера наложенных на систему связей механических. Для свободной материальной точки С. с. ч. равно 3, для свободного твёрдого тела - 6, для тела, имеющего неподвижную ось вращения, С. с. ч. равно 1 и т. д. Для любой голономной системы (системы с геом. и интегрируемыми дифференц. связями) С. с. ч. равно числу s независимых между собой координат, определяющих положение системы, и даётся равенством s = 3п - k, где п - число точек системы, k - число геом. связей. Для неголономной системы (системы, на к-рую, кроме голономных, наложены ещё неголономные, т. е. неинтегрируемые дифференц. связи) С. с. ч. меньше числа координат, определяющих положение системы, на число неголономных связей. От С. с. ч. зависит число дифференц. ур-ний движения или условий равновесия механич. системы. 19. Теплота и работа. Теплота Q представляет собой количественную меру хаотического движения частиц данной системы или тела. Энергия более нагретого тела в форме теплоты передается менее нагретому телу. При этом не происходит переноса вещества. Работа А является количественной мерой направленного движения частиц, мерой энергии, передаваемой от одной системы к другой за счет перемещения вещества от одной системы к другой под действием тех или иных сил, например гравитационных. Теплоту и работу измеряют в джоулях (Дж), килоджоулях (кДж) и мегаджоулях (МДж). Положительной считается работа, совершаемая системой против внешних сил (А > 0) и теплота, подводимая к системе (Q > 0). Теплота и работа зависят от способа проведения процесса, т.е. они являются функциями пути. Количественное соотношение между изменением внутренней энергии, теплотой и работой устанавливает первый закон термодинамики: Q = Δ U + А. Теплоту и работу можно измерить, отсюда, Δ U = Q – А. Первый закон термодинамики является формой выражения закона сохранения энергии. Согласно этому закону, энергия не может ни создаваться, ни исчезать, но может превращаться из одной формы в другую. Его справедливость доказана многовековым опытом человечества. Если система осуществляет переход из одного состояния в другое при постоянном объеме (реакция протекает в автоклаве), то работа расширения системы А = р Δ V = 0 и Q v = Δ U = U 2 – U 1, т.е. если реакция протекает при постоянном объеме, то выделение или поглощение теплоты Q связано с изменением внутренней энергии системы. Если на систему не действуют ни какие другие силы, кроме постоянного давления, т.е. химический процесс осуществляется в изобарных условиях, и единственным видом работы является работа расширения, то первый закон термодинамики запишется: Q p = Δ U + p Δ V. Подставив Δ U = U 2 ‑ U 1, получим: Q p = U 2 ‑ U 1 + pV 2 ‑ pV 1 = (U 2 + pV 2) ‑ (U 1 + pV 1). Характеристическая функция U + pV = H называется энтальпией системы. Q p = H 2 - H 1, и Q p = Δ H. В случае изобарического процесса теплота, подведенная к системе, равна изменению энтальпии системы. Абсолютное значение энтальпии системы определить невозможно, но экспериментально можно определить Q p, т.е. изменение энтальпии Δ Н, при переходе из одного состояния в другое. Н -это термодинамическая функция состояния. Если Δ Н > 0 - энтальпия системы возрастает, если Δ Н < 0-энтальпия системы уменьшается, т.е. теплота выделяется системой. Как и другие характеристические функции, энтальпия зависит от количества вещества, поэтому ее изменение Δ Н, обычно относят к 1 моль и выражают в кДж/моль.
20. Теплоемкость вещества. Когда одинаковое количество энергии передано телам равной массы, но состоящих из разных веществ, то повышение температуры этих тел неодинаково. Свойство вещества, от которого зависит различие температур тел при нагревании, называют теплоемкостью вещества. Количество теплоты, необходимое для повышения температуры тела на 10К (10С), является характеристической величиной для данного тела. Эта величина получила название теплоемкости тела. Теплоемкость тела это физическая величина, равная количеству теплоты, которое необходимо сообщить телу, чтобы изменить его температуру на 10К. Теплоемкость и сама зависит от температуры: нагрев тела от 0 до 10С, или от 99 до 1000С, требует различных количеств теплоты. Если при нагревании тела от Т1 до Т2 оно получило количество теплоты Q, то теплоемкость тела будет численно равна: Если в состав тела входит только одно вещество, то теплоемкость этого тела пропорциональна его массе: Коэффициент пропорциональности с, характеризующий данное вещество, называется его удельной теплоемкостью. Удельная теплоемкость вещества это физическая величина, численно равная количеству теплоты, необходимому для повышения температуры единицы массы (1 кг) вещества на 10К. Если при нагревании тела массой Значения теплоемкостей колеблются в довольно широких пределах. Кроме того, теплоемкости всех тел, как правило, уменьшаются с падением температуры и при температурах, близких к абсолютному нулю, принимают ничтожно малые значения. Знание теплоемкостей может пригодиться при решении различных задач о распределении тепла между телами. Различие между теплоемкостями воды и почвы является одной из причин, определяющих разницу между морским и континентальным климатом. Обладая примерно в пять раз большей теплоемкостью, чем почва, вода медленно нагревается и так же медленно отдает свое тепло.
21. Первое начало термодинамики Первое начало термодинамики — одно из основных положений термодинамики, являющееся, по существу, законом сохранения энергии в применении к термодинамическим процессам. Первое начало термодинамики было сформулировано в середине XIX века в результате работ Ю. Р. Майера, Джоуля и Г. Гельмгольца. Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя 1-го рода, который совершал бы работу, не черпая энергию из какого-либо источника. Первое начало можно сформулировать в нескольких видах: 1. Невозможно возникновение и уничтожение энергии. 2. Любая форма движения способна и должна превращаться в любую другую форму движения. 3. Внутренняя энергия является однозначной формой состояния. 4. Вечный двигатель первого рода невозможен. 5. Бесконечно малое изменение внутренней энергии является полным дифференциалом. 6. Сумма количества теплоты и работы не зависит от пути процесса. Первый закон термодинамики, постулируя закон сохранения энергии для термодинамической системы. не указывает направление происходящих в природе процессов. Направление термодинамических процессов устанавливает второе начало термодинамики. первый закон (первое начало) термодинамики можно сформулировать так: «Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты Q, сообщенного системе, в сумме с изменением энергии, связанной с количеством вещества N при химическом потенциале
Для элементарного количества теплоты
При сообщении термодинамической системе некоторого количества теплоты Q в общем случае происходит изменение внутренней энергии системы D U и система совершает работу А: Q = D U + A (1) Уравнение (1), выражающее П. н. т., является определением изменения внутренней энергии системы (D U), так как Q и А — независимо измеряемые величины. Внутреннюю энергию системы U можно, в частности, найти, измеряя работу системы в адиабатном процессе (то есть при Q = 0): А ад = — D U, что определяет U с точностью до некоторой аддитивной постоянной U0: U = U + U0 (2) П. н. т. утверждает, что U является функцией состояния системы, то есть каждое состояние термодинамической системы характеризуется определённым значением U, независимо от того, каким путём система приведена в данное состояние (в то время как значения Q и А зависят от процесса, приведшего к изменению состояния системы). При исследовании термодинамических свойств физической систем П. н. т. обычно применяется совместно со вторым началом термодинамики.
22. АДИАБАТИЧЕСКИЙ ПРОЦЕСС (адиабатный процесс) - термодинамич. процесс, происходящий в системе без теплообмена с окружающей средой Очень быстрые процессы, при к-рых не успевает произойти теплообмен с окружающей средой, напр. при распространении звука, можно рассматривать как А. п. Энтропия каждого малого элемента жидкости при его движении со скоростью u остаётся постоянной, поэтому полная производная энтропии s, отнесённой к единице массы, равна нулю, 23. ПУАССОНА УРАВНЕНИЕ - неоднородное дифференц. ур-ние в частных производных
где D - Лапласа оператор, задачи для П. у. сводятся к соответствующим задачам Лапласа уравнения подстановкой
где v удовлетворяет ур-нию Лапласа
(логарифмич. потенциал);
(ньютонов потенциал). Здесь П. у. фигурирует в обширном круге физ. задач. Ему удовлетворяют: потенциалы ньютоновых (кулоновых) сил, порождённых массами (зарядами), распределёнными в области G с плотностью PV = const. Это уравнение называется уравнением Пуассона (1781—1840). Оно является уравнением адиабаты, т. е. кривой, графически изображающей квазистатический адиабатический процесс. Величина у называется адиабатической постоянной/
|


 — Средняя квадратичная скорость молекул
— Средняя квадратичная скорость молекул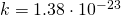 — Постоянная Больцмана
— Постоянная Больцмана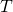 — Температура
— Температура — Масса одной молекулы
— Масса одной молекулы — Универсальная газовая постоянная
— Универсальная газовая постоянная — Молярная масса
— Молярная масса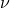 — Количество вещества
— Количество вещества — Средняя кинетическая энергия молекул
— Средняя кинетическая энергия молекул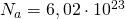 — Число Авогадро
— Число Авогадро
 , где
, где  — внутренняя энергия,
— внутренняя энергия,  — абсолютная температура,
— абсолютная температура,  — энтропия.
— энтропия. 
 — подведённое к телу количество теплоты, измеренное в джоулях
— подведённое к телу количество теплоты, измеренное в джоулях [1] — работа, совершаемая телом против внешних сил, измеренная в джоулях
[1] — работа, совершаемая телом против внешних сил, измеренная в джоулях . (1)
. (1) .
. от Т1 до Т2 оно получило количество теплоты Q, то теплоемкость вещества, из которого изготовлено это тело будет численно равна:
от Т1 до Т2 оно получило количество теплоты Q, то теплоемкость вещества, из которого изготовлено это тело будет численно равна: . (2)
. (2) , и работы A', совершённой над системой внешними силами и полями, за вычетом работы А, совершённой самой системой против внешних сил»:
, и работы A', совершённой над системой внешними силами и полями, за вычетом работы А, совершённой самой системой против внешних сил»: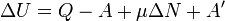 .
. , элементарной работы
, элементарной работы  и малого приращения (полного дифференциала)
и малого приращения (полного дифференциала)  внутренней энергии первый закон термодинамики имеет вид:
внутренней энергии первый закон термодинамики имеет вид: .
. , т. е. в адиабатически изолир. системе, состояние к-рой можно изменить только путём изменения внеш. параметров. Понятие адиабатич. изоляции является идеализацией теплоизолирующих оболочек или сосудов Дьюара (адиабатные оболочки). Изменение темп-ры внеш. тел не оказывает влияния на адиабатически изолир. системы, а их энергия U может изменяться только за счёт работы, совершаемой системой (или над ней). Согласно первому началу термодинамики, при обратимом А. п. для однородной системы
, т. е. в адиабатически изолир. системе, состояние к-рой можно изменить только путём изменения внеш. параметров. Понятие адиабатич. изоляции является идеализацией теплоизолирующих оболочек или сосудов Дьюара (адиабатные оболочки). Изменение темп-ры внеш. тел не оказывает влияния на адиабатически изолир. системы, а их энергия U может изменяться только за счёт работы, совершаемой системой (или над ней). Согласно первому началу термодинамики, при обратимом А. п. для однородной системы  , где V - объём системы, Р - давление, а в общем случае
, где V - объём системы, Р - давление, а в общем случае  , где
, где  - внеш. параметры,
- внеш. параметры,  - термодинамич. силы. Согласно второму началу термодинамики, при обратимом А. п. энтропия постоянна,
- термодинамич. силы. Согласно второму началу термодинамики, при обратимом А. п. энтропия постоянна,  , а при необратимом - возрастает.
, а при необратимом - возрастает.
 (условие адиабатичности). Простым примером А. п. является сжатие (или расширение) газа в теплоизолир. цилиндре с теплоизолир. поршнем: при сжатии темп-pa возрастает, при расширении - убывает. Др. примером А. п. может служить адиабатич. размагничивание, к-рое используют в методе магнитного охлаждения. Обратимый А. п., наз. также изоэнтропийным, изображается на диаграмме состояния адиабатой (изоэнтропой).
(условие адиабатичности). Простым примером А. п. является сжатие (или расширение) газа в теплоизолир. цилиндре с теплоизолир. поршнем: при сжатии темп-pa возрастает, при расширении - убывает. Др. примером А. п. может служить адиабатич. размагничивание, к-рое используют в методе магнитного охлаждения. Обратимый А. п., наз. также изоэнтропийным, изображается на диаграмме состояния адиабатой (изоэнтропой).
 Краевые
Краевые
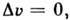 a V - фундам. решение П. у. в области G:
a V - фундам. решение П. у. в области G:

 - площадь поверхности единичной сферы в n-мерном евклидовом пространстве, Г - гамма-функция (см. Эйлера интегралы).
- площадь поверхности единичной сферы в n-мерном евклидовом пространстве, Г - гамма-функция (см. Эйлера интегралы). потенциал скоростей идеальной несжимаемой жидкости; характеристики стационарных процессов теплопроводности и диффузии. П. у. возникает также в стационарных задачах теории упругости.
потенциал скоростей идеальной несжимаемой жидкости; характеристики стационарных процессов теплопроводности и диффузии. П. у. возникает также в стационарных задачах теории упругости.


