РЕШЕНИЕ
1. Построение модели регрессии 1.1. Анализ исходных данных Построим графики зависимостей x(t), y(t), y(x) (рис. 1-3):
Рис. 1 Рис. 2
Рис. 3 Выводы: Графический анализ исходных данных показывает, что для построения прогнозной модели может быть использована _______________ модель регрессии. ____________________________________________________ ____________________________________________________________________
1.2. Построение модели регрессии y(x): В соответствии с методом наименьших квадратов (МНК) для определения коэффициентов регрессии a 0 и a 1 решим систему уравнений: na 0 + a 1S x = S y a 0S x + a1 S x 2 = S xy Для удобства вычислений параметров системы уравнений составим табл. 1. Таблица 1
Исходя из табл. 1, система уравнений численными значениями параметров имеет вид: _______ a 0 + _______ a 1 = _________ _______ a 0 + _______ a 1 = _________
Решим систему уравнений по правилу Крамера:
D0 = D1 =
D3 = a 0 = a 1 = Вывод: Модель регрессии с численными оценками коэффициентов имеет вид:
2. Анализ качества модели – анализ остатков Определим остатки по формуле (cм. табл. 2): ei = yi - Таблица 2
2.1. Визуальный анализ остатков
Вывод: Наличие выбросов в остатках ___________________________________, разброс остатков [_______; ______], что ___превышает 10% среднего y. ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ Графический анализ остатков показывает, что гипотеза о случайности и независимости остатков ____ принимается. 2.2. Анализ по критерию "серий" 2.2.1. Проверка по числу серий: S(n) > S0(n), где
_________ – __________ = __________» ______. S(n) = _____ (см. график рис. 4). S(n) ____ S0(n). Вывод: Число серий в нашем случае ___ удовлетворяет требованиям.
2.2.2. Проверка по максимальной длине серий: l(n) < l0(n), где l0(n) = 5 – по условию для n £ 26, l(n) = _____ (см. график рис. 4)
Вывод: Максимальная длина серий ___удовлетворяет критерию. Общий вывод: По критерию серий можно сделать вывод о том, что остатки ___ являются случайными и независимыми. ______________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ 2.3. Анализ по критерию Дарбина-Уотсона – оценка на отсутствие автокорреляции в остатках: Вычислим коэффициент Дарбина-Уотсона DW (промежуточные вычисления внесены в табл. 2):
Коэффициент DW является критерием проверки гипотезы о наличии автокорреляции в остатках генеральной совокупности. Значения критерия DW затабулированы. По таблице Дарбина-Уотсона находим для заданного уровня значимости a = 0,05 и числа наблюдений n = _____ теоретические значения dL = ______ и du = ______. Для сравнения табличных и расчетных значений построим схему:
+ автокорр.? автокорр.отсутств.? - автокорр. __________|___________|_______________|____________|___________| 0 dL du 4 - du 4 – dL 4 _____ _____ _____ _____
Рис. 5.
Вывод: Критерий Дарбина-Уотсона ___ подтверждает гипотезу об отсутствии автокорреляции в остатках. ____________________________________________ ____________________________________________________________________. Общие выводы: В целом, остатки ____ удовлетворяют основным требованиям регрессионного анализа. ______________________________________________ ____________________________________________________________________________________________________________________________________________________________________________________________________________
3.1. Визуальный анализ взаимосвязи показателей Проведем визуальный анализ взаимосвязи показателей x и y на основе графика корреляционного поля (рис. 6). На рисунке ____прослеживается определенная _____________ взаимосвязь в изменении значений y при изменении величин x в сторону увеличения. Форму взаимосвязи можно считать линейной. Рис. 6. Вывод: Визуальный анализ графика корреляционного поля показателей x и y показал, что взаимосвязь показателей наблюдается: с изменением одного показателя меняется другой, причем взаимосвязь _________: с увеличением показателя x наблюдается _______ показателя y. Форму взаимосвязи можно считать линейной. 3.2. Расчет коэффициента корреляции Расчет коэффициента корреляции выполним по формуле:
Промежуточные вычисления отражены в табл. 3. Таблица 3.
Величина коэффициента корреляции равна:
= ¾¾¾¾¾ = __________. Вывод: Величина коэффициента корреляции rxy = _______ свидетельствует о __________________________________ связи между показателями x и y. _______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________. 3.3. Проверка статистической значимости коэффициента корреляции Выполняем проверку статистической значимости коэффициента корреляции с помощью t -статистики:
Сравним t расч. и t табл.: t расч. ___ t табл. Вывод: Проверка статистической значимости коэффициента корреляции rxy показывает, что коэффициент ___значимо отличен от нуля. Общий вывод: Корреляционный анализ показал, что между показателями x и y имеется __________________________________ взаимосвязь. Однако следует отметить, что очевидное наличие во временных рядах x(t) и y(t) трендов (см. рис. 1, 2) ____________________________________________________________ ____________________________________________________________________________________________________________________________________________________________________________________________________________ требуют проведения более строгого корреляционного анализа взаимосвязи показателей. 4. Проверка качества модели регрессии. 4.1. Анализ коэффициентов регрессии 4.1.1. Вычисление среднеквадратической ошибки коэффициентов регрессии.
где b22 = n / D 0 = ___ / __________ = ________ (см. п. 1.2);
Вывод: Среднеквадратическая ошибка коэффициента регрессии a 1 равна _______.
4.1.2. Проверка статистической значимости коэффициентов регрессии. Рассчитаем значение t -статистики t расч и сравним с t табл.
Вывод: Коэффициент модели регрессии статистически ___значим. Фактор x оказывает статистически ___значимое воздействие на изменение y. Его следует ______________ в модели. 4.1.3. Построение доверительных интервалов для коэффициентов регрессии a 1 – t табл .× Sa 1 £ α;1 £ a 1 + t табл .× Sa 1
_________ – _______________ £ α; 1 £ _________ + _______________ ________ £ α; 1 £ _________
Вывод: Доверительный интервал для истинного коэффициента регрессии α;1– [________; ________]. Общий вывод: Коэффициент регрессии a 1статистически ______значим. Доверительный интервал для α;1 – [________; ________].
4.2. Проверка адекватности модели – анализ качества модели в целом. 4.2.1. Определение коэффициента детерминации. R 2 = 1 –
где S e 2= _________ (см. табл. 2); Для расчета S(y –` y)2 составим табл. 4 (где первые 6 столбцов перенесены из табл. 2). Среднее значение показателя (см. табл. 4): `y = Таблица 4.
R 2 = 1 – ¾¾¾¾¾¾ = ____________» ________. Вывод: На ____% вариация признака y (__________________________________ ___________________________________________________________________) объясняется влиянием фактора x (___________________________________).
4.2.2. Оценка статистической значимости R 2 Проверяем нулевую гипотезу о том, что коэффициент детерминации в генеральной совокупности равен нулю. Проверку гипотезы осуществляем с помощью F -критерия (критерия Фишера). Для k =1 – число факторов в модели:
F расч. =
F табл .(a, n-k- 1, k) = t табл.(0,05; __; __) = ______.
½ F расч.½ ____ F табл.(a, n-k- 1, k).
Вывод: Проверка статистической значимости коэффициента детерминации R 2 показывает, что R 2 ___значимо отличается от нуля. Нулевая гипотеза ___ отклоняется с заданным уровнем доверительной вероятности a = 0,05. Общий вывод: Построенная для прогноза регрессионная модель ___ адекватна. 5. Экстраполяция по отношению к признаку x 5.1. Графический анализ Визуальный анализ графика x(t) рис.1 ___дает основание для выбора линейной модели тренда: x(t) = a 0 + a 1 t. Вывод: На основе графического анализа можно выдвинуть гипотезы: а) о наличии _________________ тенденции (____________ тренда), б) линейности тренда. Проверим гипотезы с использованием аналитических методов.
5.2. Аналитические критерии оценки временного ряда. Выбор модели тренда. Проведем углубленный анализ данных временного ряда x(t). 5.2.1. Анализ данных на наличие тренда по критерию Кендела Таблица 5
Рассчитаем критерий Кендела для временного ряда x(t): t = где p = _____ (см. табл. 5), n = _____. t = ¾¾¾¾¾ – 1 = ________.
Вывод: Коэффициент t = _____, значит, в соответствии с критерием Кендела, __________________ тенденция ______выражена.
5.2.2. Проверка статистической значимости t Проверим статистическую значимость t. Для этого найдем:
где zкр = 1,96 для заданного уровня значимости a = 0,05. Тогда:
Сравнивая t с Tкр, получим: ½ t ½___ Tкр, следовательно, t статистически ____значим. Вывод: t ___ Tкр . Þ t – статистически ___значим. Общий вывод: Аналитический способ установления тренда во временном ряду x(t) с помощью критерия Кендела ___ подтвердил гипотезу о наличии тренда. ___________________ знак t свидетельствует о наличии __________________ тенденции. Таким, образом, временной ряд x(t) ___ имеет ____________ тренд. 5.3. Определение формы зависимости тренда (подтверждение гипотезы о линейности тренда) Для проверки линейности тренда воспользуемся методом конечных разностей (табл. 6): Таблица 6
Вывод: Средняя арифметическая ________ конечных разностей близка к нулю. Метод конечных разностей __подтверждает линейность тренда. ___________________________________ ____________________________________________________________________________________ Общий вывод: Аналитические критерии оценки временного ряда x (t) ___ подтверждают наличие в нем ____________ линейного тренда. Для последующего анализа продолжим использовать модель линейного тренда:
5.4. Определение параметров тренда Для определения параметров тренда a 0 и a 1 используем МНК, в соответствии с которым решим систему уравнений:
na 0 + a 1S t = Sx a 0S t + a 1S t2 = S tx. Необходимые расчеты числовых значений коэффициентов системы линейных уравнений отражены в табл. 7. _____ a 0 + _____ a 1 = ______ _____ a 0 + _____ a 1 = ______ _____ a 0 + _____ a 1 = ______ Þ _____ a 0 + _____ a 1 = ______ Þ
Þ ______ a 1 = _______ Þ a 1 = _______.
a 0 = (__________ – __________) / ___ = ______ / ___ = _________. Вывод: Таким образом, линейное уравнение тренда имеет вид:
5.5. Проверка качества модели тренда Проверим качество полученной модели на основе оценки средней относительной погрешности:
Промежуточные расчеты отражены в табл. 7. Таблица 7
Вывод: Относительная погрешность ______% ___________значительная. Модель ___адекватна. Общий вывод: Линейное уравнение тренда имеет вид:
Качество модели __________удовлетворительное. Модель ___ может быть использована для прогноза. 5.6. Прогноз признака x – _________________________________ ( t = ____):
Вывод: Ожидаемый _____________________________________ – ~ _________. 5.7. Прогноз фактора y – ______________________________________________ ( t = ____). Модель регрессии с численными коэффициентами имеет вид:
Для прогнозируемого x = __________ получим:
Вывод: ____________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________
Общие выводы по результатам проведенного эконометрического анализа ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ ___________________________________________________________________ 6. Углубленный корреляционный анализ взаимосвязи показателей x и y.
Углубленный корреляционный анализ взаимосвязи показателей x и y необходимо провести в силу того, что: 1) корреляционный анализ разработан для оперирования со случайными выборками, тогда как анализируемые показатели x и y представлены временными рядами, явно содержащими тренды (см. рис 1, 2); 2) __________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ Проверим гипотезу о том, что вычисленный выше (см. п.3) коэффициент корреляции взаимосвязи показателей rxy = _______ содержит ложную корреляцию, объясняемую влиянием показателя времени t, неучтенного явно в модели регрессии Для исключения влияния фактора времени t при оценке взаимосвязи признаков x и y применим корреляционный анализ не к самим показателям x и y, а к их отклонениям от соответствующих трендов, т.е. к ex = x(t) –
7.1. Определение уравнений трендов Уравнение тренда для показателя x(t) было получено выше (см. 5.4):
Определим уравнение тренда для показателя y. Исходя из графика y(t) (см. рис.2) делаем предположение о линейности тренда:
Используя метод наименьших квадратов, определим параметры тренда a0, a1, решая систему линейных уравнений:
na 0 + a 1S t = S y a 0S t + a 1S t 2 = S ty. Необходимые расчеты отражены в табл. 8. Таблица 8.
Решая систему уравнений:
______ a 0 +_______ a 1 =________ ______ a 0 +_______ a 1 =________,
определим параметры тренда: a 0= _________, a 1 = _________. Таким образом, уравнение тренда для показателя y:
7.2. Определение отклонений от трендов – остатков и расчет коэффициента корреляции в остатках Найдем отклонения от трендов (табл. 9) и выполним необходимые дополнительные вычисления для определения коэффициента корреляции в остатках Таблица 9.
Таблица 10. Величина коэффициента корреляции
= ¾¾¾¾¾¾ = __________» ______.
Вывод: Величина коэффициента корреляции в остатках 7.3. Проверка статистической значимости коэффициента корреляции в остатках Выполняем проверку статистической значимости коэффициента корреляции
» ______.
t расч. ___ t табл. Вывод: Проверка статистической значимости коэффициента корреляции между отклонениями ex, ey показывает, что коэффициент корреляции ___значимо отличен от нуля. Гипотеза о наличии ложной корреляции между x и y ________________. Таким образом, Углубленный корреляционный анализ показывает, что взаимосвязь между отклонениями ex, ey фактических значений x и y от соответствующих трендовых значений Общий вывод: Углубленный корреляционный анализ показывает, что взаимосвязь между отклонениями ex, ey фактических значений x и y от соответствующих трендовых значений _________________ существенная линейная взаимосвязь анализируемого результирующего признака y с фактором x: ____________________________________________________________________ ____________________________________________________________________ ________________________________________________________________________________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ Таким образом, полученная ранее модель регрессии ____ может быть использована для целей прогнозирования. _________________ ____________________________________________________________________ ____________________________________________________________________ ________________________________________________________________________________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ Замечания:
Рекомендовано к изданию Редакционно-издательским советом Национального института бизнеса
©Национальный институт бизнеса 2009 ©Москинова Г.И. 2009
|



 = a 0 + a 1 x.
= a 0 + a 1 x.
 ¾¾¾¾ = __________,
¾¾¾¾ = __________, ¾¾¾¾ = __________.
¾¾¾¾ = __________.
 Рис. 4
Рис. 4 =
=  =
= = ¾¾¾¾ = __________» ______.
= ¾¾¾¾ = __________» ______. 3. Корреляционный анализ.
3. Корреляционный анализ. .
. = ¾¾¾¾¾¾¾¾¾¾¾¾¾¾ = ¾¾¾¾ =
= ¾¾¾¾¾¾¾¾¾¾¾¾¾¾ = ¾¾¾¾ = = ¾¾ × ¾¾¾¾¾ = ________» ______.
= ¾¾ × ¾¾¾¾¾ = ________» ______. t табл. (a = 0,05; n-k -1 = __) = _____.
t табл. (a = 0,05; n-k -1 = __) = _____. ,
, = _________ (см. табл. 2).
= _________ (см. табл. 2). =
=  = ________.
= ________.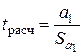 = ¾¾¾¾¾» ________.
= ¾¾¾¾¾» ________. = ________.
= ________. ___
___ 
 ,
, S y = ________.
S y = ________.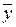
 = ¾¾¾¾¾¾ = ____________» ______.
= ¾¾¾¾¾¾ = ____________» ______. ,
, ,
, =
=  = __________» _______.
= __________» _______. (t) = a 0 + a 1 t
(t) = a 0 + a 1 t
 (t)
(t)
 = ¾¾¾¾¾» ________.
= ¾¾¾¾¾» ________. .
. (табл. 10).
(табл. 10). = ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ =
= ¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ =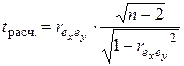 =
= 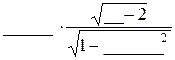 = ¾¾¾¾¾¾ = _________»
= ¾¾¾¾¾¾ = _________»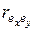 = ______. Вычисленный ранее коэффициент корреляции rxy = _______ отражает __________________________
= ______. Вычисленный ранее коэффициент корреляции rxy = _______ отражает __________________________


