Формула полной вероятности и формула Байеса
Если событие А может произойти только при выполнении одного из событий
Эта формула называется формулой полной вероятности. Вновь рассмотрим полную группу несовместных событий
Если событие А произошло, то это может изменить вероятности гипотез По теореме умножения вероятностей
откуда
Аналогично, для остальных гипотез
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез Пример. В магаз поступила новая продукция с 3х предприятий.20%-продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта. Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через Можно применить формулу полной вероятности, причем в наших обозначениях:
Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:
Пример. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком. Решение. Возможны три гипотезы: А1 - на линию огня вызван первый стрелок, А2 - на линию огня вызван второй стрелок, А1 - на линию огня вызван третий стрелок. Так как вызов на линию огня любого стрелка равновозможен, то В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:
по формуле Байеса находим вероятность гипотезы
Пример. На трех станках-автоматах обрабатываются однотипные детали, поступающие после обработки на общий конвейер. Первый станок дает 2% брака, второй – 7%, третий – 10%. Производительность первого станка в 3 раза больше производительности второго, а третьего – в 2 раза меньше, чем второго. а) Каков процент брака на конвейере? б) Каковы доли деталей каждого станка среди бракованных деталей на конвейере? Решение. Возьмем с конвейера наудачу одну деталь и рассмотрим событие А – деталь бракованная. Оно связано с гипотезами относительно того, где была обработана эта деталь: Условные вероятности (в условии задачи они даны в форме процентов):
Зависимости между производительностями станков означают следующее:
А так как гипотезы образуют полную группу, то Решив полученную систему уравнений, найдем: а) Полная вероятность того, что взятая наудачу с конвейера деталь – бракованная:
Другими словами, в массе деталей, сходящих с конвейера, брак составляет 4%. б) Пусть известно, что взятая наудачу деталь – бракованная. Пользуясь формулой Байеса, найдем условные вероятности гипотез:
Таким образом, в общей массе бракованных деталей на конвейере доля первого станка составляет 33%, второго – 39%, третьего – 28%.
|

 , которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле
, которые образуют полную группу несовместных событий, то вероятность события А вычисляется по формуле .
. . Событие А может произойти только вместе с каким-либо из событий
. Событие А может произойти только вместе с каким-либо из событий 
 ,
, .
.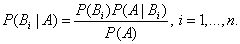
 называются апостериорными вероятностями, тогда как
называются апостериорными вероятностями, тогда как  - априорными вероятностями.
- априорными вероятностями.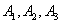 обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.



 после опыта:
после опыта:
 – взятая наудачу деталь обработана на
– взятая наудачу деталь обработана на 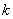 -ом станке,
-ом станке, 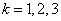 .
.
 .
. .
. .
. .
. ,
, ,
, .
.


