Решение. А – формула содержится в первом справочнике;
А – формула содержится в первом справочнике; В – формула содержится во втором справочнике; С – формула содержится в третьем справочнике. Воспользуемся теоремами сложения и умножения вероятностей. 1. 2. 3. Пусть в результате испытания могут появиться n событий, независимых в совокупности, либо некоторые из них (в частности, только одно или ни одного), причем вероятности появления каждого из событий известны. Как найти вероятность того, что наступит хотя бы одно из этих событий? Например, если в результате испытания могут появиться три события, то появление хотя бы одного из этих событий означает наступление либо одного, либо двух, либо трех событий. Ответ на поставленный вопрос дает следующая теорема. Теорема. Вероятность появления хотя бы одного из событий
Если события
Пример. Вероятности попадания в цель при стрельбе из трех орудий таковы: p 1 = 0,8; p 2 = 0,7; p 3 = 0,9. Найти вероятность хотя бы одного попадания (событие А) при одном залпе из всех орудий. Решение. Вероятность попадания в цель каждым из орудий не зависит от результатов стрельбы из других орудий, поэтому рассматриваемые события Вероятности событий, противоположных событиям
Искомая вероятность Пример. В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент, равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина (событие А). Решение. События "машина работает" и "машина не работает" (в данный момент) — противоположные, поэтому сумма их вероятностей равна единице: Отсюда вероятность того, что машина в данный момент не работает, равна Искомая вероятность Так как полученная вероятность весьма близка к единице, то на основании следствия из принципа практической невозможности маловероятных событий мы вправе заключить, что в данный момент работает хотя бы одна из машин. Пример. Вероятность того, что при одном выстреле стрелок попадает в цель, равна 0,4. Сколько выстрелов должен произвести стрелок, чтобы с вероятностью не менее 0,9 он попал в цель хотя бы один раз? Решение. Обозначим через А событие "при n выстрелах стрелок попадает в цель хотя бы один раз". События, состоящие в попадании в цель при первом, втором выстрелах и т. д., независимы в совокупности, поэтому применима формула Приняв во внимание, что, по условию,
Прологарифмируем это неравенство по основанию 10:
Итак,
|


 .
.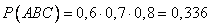
 , независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий
 , то формула принимает простой вид:
, то формула принимает простой вид: .
. (попадание первого орудия),
(попадание первого орудия),  (попадание второго орудия) и
(попадание второго орудия) и  (попадание третьего орудия) независимы в совокупности.
(попадание третьего орудия) независимы в совокупности. ,
, 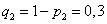 ,
, 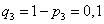
 .
.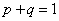


 .
. (следовательно,
(следовательно, 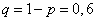 ), получим
), получим

 , т.е. стрелок должен произвести не менее 5 выстрелов.
, т.е. стрелок должен произвести не менее 5 выстрелов.


