Сложение и умножение вероятностей
Событие А называется частным случаем события В, если при наступлении А наступает и В. То, что А является частным случаем В, записываем События А и В называются равными, если каждое из них является частным случаем другого. Равенство событий А и В записываем А = В. Суммой событий А и В называется событие А + В, которое наступает тогда и только тогда, когда наступает хотя бы одно из событий: А или В. Теорема о сложении вероятностей. Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий.
Заметим, что сформулированная теорема справедлива для любого числа несовместных событий:
Если случайные события
Произведением событий А и В называется событие АВ, которое наступает тогда и только тогда, когда наступают оба события: А и В одновременно. Случайные события А и B называются совместными, если при данном испытании могут произойти оба эти события. Теорема о сложении вероятностей 2. Вероятность суммы совместных событий вычисляется по формуле
События событий А и В называются независимыми, если появление одного из них не меняет вероятности появления другого. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет. Теорема об умножении вероятностей. Вероятность произведения независимых событий А и В вычисляется по формуле:
Вероятность произведения зависимых событий вычисляется по формуле условной вероятности (см. следующий раздел). Пример. В первом ящике 1 белый и 5 черных шаров, во втором 8 белых и 4 черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный. Решение. Обозначим события: А – вынули белый шар из первого ящика,
В – белый шар из второго ящика,
Нам нужно, чтобы произошло одно из событий Пример. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания; г) одного попадания.
|

 .
.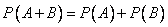
 .
. образуют полную группу несовместных событий, то имеет место равенство
образуют полную группу несовместных событий, то имеет место равенство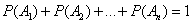 .
. .
. .
. ;
; - вынули черный шар из первого ящика,
- вынули черный шар из первого ящика,  ;
; ;
; - черный шар из второго ящика,
- черный шар из второго ящика,  .
. или
или  . По теореме об умножении вероятностей
. По теореме об умножении вероятностей ,
, 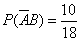 .
.  .
.


