Уравнение адсорбции Генри
Уравнение количественно описывающие процесс адсорбции называют именами их авторов. При выводе этого уравнения поверхностный слой будем рассматривать, как отдельную фазу. Перераспределение вещества между поверхностным слоем и объемом фазы будет происходить до тех пор, пока химические потенциалы в поверхностном слое и объеме фазы не выравняются, т.е. μ=μs (1) Где μs – химический потенциал вещества в поверхностном слое; μ- химический потенциал для объемной фазы. Если μ если μ Учитывая, что μ= μ0+ RT∙ln a, (2) μs= где а- активность адсорбата в объемной фазе; as- активность адсорбата на поверхности. Подставляя (2) и (3) в (1), получаем: μ 0 + RT∙ln a = Преобразуя, имеем:
Константа Kг- называется константой распределения Генри. Она не зависит от концентрации, а зависит только от температуры- Kг= f(Т). Если в области малых концентраций активность можно считать равной концентрации (а = с, аs= сs), то поверхностная концентрация Сs =А. Из уравнения (5) будем иметь:
Учитывая то, что P=C∙R∙T; C= Можно получить выражение адсорбции через давление: А= Уравнение (6) и (7) выражают Закон Генри для адсорбции: величина адсорбции при малых давлениях газа (концентрации раствора) пропорциональна давлению (концентрации). Данное уравнение простое, но иногда его вполне достаточно для практических расчетов. На твердых поверхностях область действия закона мала из-за неоднородности поверхности. Но даже на однородной поверхности обнаруживается отклонение от линейной зависимости при увеличении Р или С. Это объясняется уменьшением доли свободной поверхности, приводящим к замедлению роста адсорбции. А
Р(С) Отклонение от закона Генри учитывает эмпирическое уравнение адсорбции, установленное Фрейндлихом. Уравнение имеет вид: для адсорбции газов: А= для адсорбции из растворов: А= где х- количество адсорбированного вещества; m- масса адсорбента; Р,С- равновесные давление или концентрация; К, К’,1/n- константы, причем n Для газов 1/n= 0,2- 0,9, для растворов: 1/n=0,2- 0,5. Величина n характеризует степень отклонения изотермы от линейности. Рассмотрим, какие участки изотермы адсорбции описывает уравнение Фрейндлиха.
А I II III
Д Е
B А
Р(С) О
На участке ОВ адсорбция прямопропорциональна концентрации, для него постоянная 1/n должна быть равна единице. На участке ДЕ- наблюдается независимость адсорбции от концентрации. Чтобы уравнение (1) описывало этот участок, необходимо, чтобы 1/n=0, но в уравнении Фрейндлиха 1/n- дробная величина. Следовательно, это уравнение справедливо только для переходной части изотермы на участке ВД, т.е. для области средних концентраций, где 0 Таким образом уравнение Фрейндлиха, описывает только переходную часть изотермы, и не определяет предельную адсорбцию А Начальный участок ОВ – подчиняется уравнению Генри. Уравнение Фрейндлиха используется широко на практике, но только для ориентировочных расчетов. Схематически изотерма адсорбции имеет вид: А
2 3 С(Р) 1 участок – круто поднимающийся вверх, почти прямолинейный, показывает, что при малых давлениях (или С) адсорбция растет линейно или пропорционально этим величинам: А = К ∙ С или А = К ∙ Р 3 участок – горизонтальный, соответствующий большим давлениям (или С), поверхность адсорбента полностью насыщена адсорбтивом: А = К1 2 участок – средний участок кривой соответствует промежуточным степеням заполнения поверхности: А = К ∙С1/n, где 0 < используется для аналитического выражения изотермы адсорбции
|

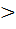 μs, то адсорбция положительная,
μs, то адсорбция положительная,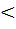 μs, то адсорбция отрицательная.(вещество уходит с поверхности.)
μs, то адсорбция отрицательная.(вещество уходит с поверхности.) + RT∙ln as, (3)
+ RT∙ln as, (3) = const= Kг (5)
= const= Kг (5) = Кг или А= Кг ∙С (6)
= Кг или А= Кг ∙С (6) ,
, или А= Кг’∙P (7)
или А= Кг’∙P (7) = К∙Р1/n (1)
= К∙Р1/n (1)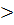 1, т.е. 1/n
1, т.е. 1/n  1.
1.
 <1 - эмперическое уравнение Фрейндлиха,
<1 - эмперическое уравнение Фрейндлиха,


