Классификация адсорбционных процессов
Основна: 1. Паращук Г. П. та ін. «Внутрішні хвороби» К. Здоров’я 1994р. с. 102-123 2. Шевчук М. Г. «Сестринська справа» К. Здоров’я 1992р. с. 357-361 3. Мухіна С. А Тарнавська І. І. «Теоретичні основи сестринської справи» М: Родник 1998р. с. 107-133 Додаткова: 1. Шабанов Т. Б. «Туберкульоз» М: Медицина 1981р. с. 73-137 2. Семененков Ю. Л. «Плеврити» К. Здоров’я 1983р. с. 47-83 3. «Справочник по пульмонологии» под. ред.. Илькович И. И. М: «Медицина» 1988г. с. 133-135, с. 183-203
План. 1 Работа силы; 2 Кинетическая энергия; 3 Потенциальная энергия; 4 Закон сохранения механической энергии; 5 Диссипативные системы. Закон сохранения и превращения энергии.
1 Работа А равна скалярному произведению силы A=(F,Δ Если сила изменяется, то, рассматривая элементарное перемещение d - δA=(F,d где dS=
Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ: - A= Если зависимость силы от пути представлена графически, то работа измеряется площадью, заштрихованной на рисунке:
Сила, действующая на тело, не выполняет работу, если: А) тело пребывает в покое Б) сила перпендикулярна к направлению перемещения тела Если на тело, которое движется поступательно, одновременно действуют несколько сил, то работа равнодействующей силы равна алгебраической сумме работ составляющих сил. Сила называется консервативной или потенциальной, если работа А, которая выполняется этой силой при перемещении из положения 1 в положение 2, не зависит от того по какой траектории произошло это перемещение: Примерами консервативных сил является сила тяжести, гравитационные силы, силы упругости, силы электростатического взаимодействия между заряженными телами. 2 Кинетической энергией механической системы называется энергия движения этой системы. Сила F, действующая на тело в состоянии покоя и вызывающая его движение, выполняет работу. При этом энергия подвижного тела возрастает на величину выполненной работы: dЕк=δА Запишем 2-ой закон Ньютона в скалярной форме; умножив обе части на элементарный путь dS: m Поскольку v = δА = FdS = mvdv = dEк і Ек = Кинетическая энергия зависит от величины массы и скорости движения тела. Величина кинетической энергии системы зависит от выбора системы отсчета, то есть является величиной относительной. Потенциальной энергией механической системы называют энергию, зависящую от взаимного расположения всех материальных точек системы и характера консервативных сил, действующих между точками. Работа А12, выполняемая консервативными силами при изменении расположения точек системы, определяется начальной и конечной конфигурацией системы. То есть работу А12 можно представить в виде разности значений некоторой функции, называемой потенциальной энергией. А12=Еп1-Еп2=-(Еп2-Еп1) Соответственно элементарная работа dА консервативных сил при малом изменении конфигурации системы: dА=-dЕп или (F,dґ) =-dЕп Проинтегрировав, получаем: Еп = - С – постоянная интегрирования. 1) потенциальная энергия материальной точки в поле тяжести Земли. Определяется по формуле: Еп = mgh, где h – высота тела над поверхностью Земли Около поверхности Земли Еп=0. 2) Потенциальная энергия материальной точки в поле центральных сил. Центральными называются силы, если они направлены вдоль прямых, проходящих через одну и ту же неподвижную точку – центр сил и зависят лишь от расстояния ґ до центра сил. Eп = Считается, что Еп ( 3) Потенциальная энергия упруго деформированного тела. Во время деформации упругого тела в нем возникают внутренние силы, препятствующие деформации тела и называемые силами упругости F = kx где k – коэффициент упругости. Потенциальная энергия Еп = 4 Рассмотрим, как изменяются кинетическая и потенциальная энергия какой-либо изолированной системы, в которой действуют лишь консервативные силы. Элементарная работа dА консервативных сил равна взятому с противоположным знаком элементарному изменению потенциальной энергии –dEп или изменению кинетической энергии dEк: dА = dЕк и dA = -dEп Значит dА=dЕк= - dЕп Или d(Ек+Еп)=0 Откуда: Ек+Еп=сопst Это равенство является выражением закона сохранения механической энергии, который утверждает, что полная механическая энергия консервативной системы не изменяется. 5 Существует еще один вид систем диссипативные системы, в которых механическая энергия постепенно уменьшается за счет превращения в другие формы энергии. Процесс этот называют диссипацией энергии. При “исчезновении” механической энергии всегда возникает эквивалентное количество энергии другого вида. В этом физическая суть закона сохранения и превращения энергии. Энергия никогда не исчезает и не появляется снова, она лишь превращается из одного вида в другой. Контрольные вопросы.
1. В сем заключается отличие между понятиями энергии и работы? 2. Дайте определение консервативной силы. 3. Чему равна работа консервативной силы вдоль замкнутой траектории? 4. Дайте определение кинетической и потенциальной энергии. 5. Сформулируйте закон сохранения механической энергии. Что называется энергией диссипации Классификация адсорбционных процессов. В зависимости от природы адсорбционных сил, адсорбция может быть физической и химической. Физическая адсорбция обусловлена силами межмолекулярного взаимодействия (т.е. если молекулы полярные, возникают ориентационное, индукционное и дисперсионное взаимодействия; если неполярные молекулы - возможны только дисперсионные взаимодействия).
|

 на перемещение Δ
на перемещение Δ 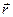 :
: cosα;
cosα; – элементарный путь.
– элементарный путь.
 cosα
cosα 
 dS = FdS
dS = FdS , то
, то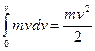


 ) = 0
) = 0



