Основные теории адсорбции
Имеется несколько теорий объясняющие физическую и химическую адсорбции. Рассмотрим первую из них: Теория мономолекулярной адсорбции Ленгмюра. Отметим основные положения этой теории. 1. Адсорбция мономолекулярна и локализована. 2. Адсорбция происходит не на всей поверхности твердого тела, а только на активных центрах адсорбции. Такими центрами являются пики и возвышения, имеющиеся даже на самой гладкой поверхности (тонко отполированное зеркало имеет выступы на поверхности – до 3 ∙107 см). 3. Один активный центр может адсорбировать только одну молекулу, в результате образуется мономолекулярный слой. 4. Адсорбированные молекулы удерживаются активными центрами только в течение определенного промежутка времени. Через некоторое время молекулы отрываются от поверхности адсорбента и переходят в газовую фазу. Взамен этих молекул активные центры могут адсорбировать новые молекулы, которые в свою очередь десорбируются и т.д., то есть имеется равновесие: десорбция ↔ адсорбция. Исходя из приведенных положений, Ленгмюр дал общее уравнение адсорбции(для газов): Г = Г Г К – константа адсорбированного равновесия; Р – равновесное давление газа.
Уравнение 1,выраженное через степень заполнения (θ): θ = КР/(1+КР) (2) Саму степень заполнения определяют: θ = Для растворов уравнение Ленгмюра имеет вид: Г= Более строгим уравнением адсорбции служит уравнение: Р = С помощью теории мономолекулярной адсорбции можно описать ступенчатую адсорбцию, изотерма которой выглядит следующим образом: А II I (1) Р Такой характер объясняется, если принять, что на поверхности адсорбента имеются группы активных центров, резко отличающихся по своей активности. Так I ступень – отвечает заполнению более активных центров; II ступень – заполнению следующих по активности центров. Данное уравнение Ленгмюра можно использовать только при условии, что адсорбция вещества сопровождается образованием мономолекулярного слоя. Это условие выполняется достаточно строго при хемосорбции и физической адсорбции газов при небольших давлениях и температурах выше критической. Встречаются и S – образные изотермы, на которых нет участка, параллельного оси давлений, и отвечающего насыщению поверхности адсорбента молекулами адсорбтива. В связи с необходимостью объяснения характера таких изотерм возникла потребность в других теориях. А II А А max I P Теория полимолекулярной адсорбции Поляни. В точке А изотерма, показанная на рис.2 круто поднимается к верху, это указывает на то, что связывание адсорбтива с адсорбентом после образования молекулярного слоя не прекращается. Для объяснения этого Поляни в 1915г. Предложил теорию полимолекулярной адсорбции (особенно пригодна при адсорбции паров на твердых телах называемой потенциальной). Основные положения теории Поляни: 1) Адсорбция обусловлена за счет физических сил; 2) На поверхности адсорбента нет активных центров, а адсорбционные силы действуют вблизи поверхности и образуют около этой поверхности непрерывное силовое поле; 3) Адсорбционные силы действуют на сравнительно большие расстояния, превышающие размеры отдельных молекул адсорбтива и поэтому можно говорить о существовании у поверхности адсорбента адсорбционного объема, которой заполняется молекулами адсорбтива;
Рис. Схема адсорбционного объема по теории Поляни.
Θ0 Θ1 Θ2 Адсорбц. Θ3 объем θ4 (макс)
θ – адсорбционный потенциал – работа, совершаемая против адсорбционных сил при перемещении 1 моля адсорбтива (пара) из данной точки поля в газовую фазу; Θ1, Θ2, Θ3!!!!!!!- поверхности с одним и тем же адсорбционным потенциалом, поэтому она называется потенциальной адсорбцией. ℓ - расстояние от поверхности. 4) Действие адсорбционных сил по мере удаления от поверхности уменьшается и на некотором расстоянии становится равным нулю; 5) Притяжение данной молекулы поверхностью адсорбента не зависит от наличия в адсорбционном пространстве других молекул; 6) Адсорбционные силы не зависят от температуры и, следовательно, с изменением температуры адсорбционный объем не изменяется; 7) Под воздействием адсорбционного поля возникает возможность образования нескольких слоев молекул адсорбата. Наибольшее притяжение и сжатие испытывает первый адсорбционный слой; газообразные продукты в нем конденсируются в жидкость. Данная теория позволяет описать адсорбцию на пористых адсорбентах и качественно объяснить характер S-образной изотермы. Но эта теория не привела к выводу уравнение, описывающего эту изотерму. Следует отметить также, что обе теории (Ленгмюра и Поляни) ограничены в применении. В зависимости от природы адсорбента и адсорбтива, от условий адсорбции – в одних случаях применима одна, в других – другая. Делались попытки обобщить представления Ленгмюра и Поляни, и описать изотермы различной формы с помощью одного уравнения. Такая теория была Б рунауэр Разработана в 40- Э ммет Теория БЭТ Х годах 20 века Т еллер Схема теории БЭТ:
- молекулы адсорбтива в первом слое;
- молекулы адсорбтива в последующих слоях; - активные центры адсорбента. Основные положения: 1) На поверхности адсорбента имеются активные центры, каждый из которых удерживает одну молекулу. 2) Молекулы первого слоя являются активными центрами для молекул второго слоя, во втором – для третьего и т.д. 3) Молекулы удерживаются в адсорбционных слоях за счет дальнодействующих сил физической природы, то есть химическое взаимодействие отсутствует. 4) Молекулы в адсорбционных слоях друг с другом не взаимодействуют. Предполагая многослойную адсорбцию ученые вывели уравнение:
где V-общий объем адсорбированного газа; Vm – объем адсорбированного газа, если вся поверхность адсорбента покрыта сплошным мономолекулярным слоем; P – равновесное давление адсорбированного газа; Ps – давление насыщения пара; С - константа при данной температуре. Согласно данному уравнению зависимость ( на графике дает прямую линию с тангенсом угла наклона (
|

 , где Г – количество газа адсорбированного 1г адсорбента или 1см2 его поверхности;
, где Г – количество газа адсорбированного 1г адсорбента или 1см2 его поверхности; - максимальное количество газа, которое может адсорбировать 1г адсорбента (1см2 его поверхности) при данной температуре;
- максимальное количество газа, которое может адсорбировать 1г адсорбента (1см2 его поверхности) при данной температуре; (3)
(3)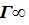 ×
× 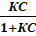 (4), где С- равновесная концентрация адсорбированного вещества в растворе.
(4), где С- равновесная концентрация адсорбированного вещества в растворе. (5), где К – константа, учитывающая силы притяжения между молекулами адсорбата.
(5), где К – константа, учитывающая силы притяжения между молекулами адсорбата.
 ) от (
) от ( )
) )
)


