Решение. Найдём множества и , используя определения операций над множествами
Найдём множества
Тогда
Тогда Поскольку множества Поскольку между элементами множеств Поскольку все элементы множества Поскольку все элементы множества Множества
Задача 2
В шахматном турнире по круговой системе участвуют семь шахматистов. Известно, что игрок С кем сыграл игрок
|
и 
, и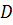спользуя определения операций над множествами.
.
), то множества 
.
.
сыграл шесть партий, 
– пять, 
и 
– по две, а 
– одну.
