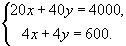Задача о выпуске продукции
Фирма выпускает два вида древесно-стружечных плит - обычные и улучшенные. При этом производится две основные операции - прессование и отделка. Требуется указать, какое количество плит каждого типа можно изготовить в течение месяца так, чтобы обеспечить максимальную прибыль при следующих ограничениях на ресурсы (материал, время, затраты):
Перейдем к построению математической модели поставленной задачи. Введем следующие обозначения. Пусть х - количество партий в 100 плит обычного вида, изготавливаемых в течение месяца; у - количество партий в 100 плит улучшенного качества, изготавливаемых в течение месяца. Тогда ожидаемую прибыль можно записать так:
Требуется найти такие значения х и у, подчиненные условиям
для которых
Для того, чтобы найти в первой четверти плоскости хОу множество точек, координаты (х, у) которых удовлетворяют указанным выше неравенствам, необходимо сначала построить прямые (по точкам их пересечения с координатными осями)
а затем, используя точку начала отсчета О (0, 0), определить соответствующие полуплоскости. Пересечением полученных полуплоскостей будет четырехугольник ОВМЕ. Наша целевая функция достигает наибольшего значения в одной из вершин четырехугольника. Нам необходимо найти координаты точки М - точки пересечения прямых EF и АВ, для этого надо решить систему уравнений
Вычислить значения z в точках В (0, 100), Е (150, 0), М (100, 50):
Из полученных значений выберем наибольшее и получим ответ:
|