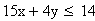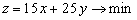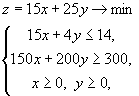Задача о диете
Исторические задача о диете является одной из первых задач линейного программирования. Постановка задачи - первый и наиболее важный этап построения модели, способный обеспечить правильное решение проблемы. Даме необходимо похудеть, за помощью обратилась к подруге. Построение модели - рассмотрение этого этапа и является главной целью. Подруга посоветовала перейти на рациональное питание, состоящее из двух продуктов P и Q. Суточное питание этими продуктами должно давать не более 14 единиц жира (чтобы похудеть), но не менее 300 калорий. На упаковке продукта Р написано, что в одном килограмме этого продукта содержится 15 единиц жира и 150 калорий, а на упаковке с продуктом Q - 4 единицы жира и 200 калорий соответственно. При этом цена 1 килограмма продукта Р равна 15 руб., а 1 кг продукта Q - 25 руб. Так как дама была стеснена в средствах, но ее интересовал вопрос: в какой пропорции нужно брать эти продукты для того, чтобы выдержать условия диеты и истратить как можно меньше денег? Перейдем к формализации данной ситуации на языке математических символов. Обозначим через х количество продукта Р и через у количество продукта Q, требуемые для выполнения условий диеты. Количество единиц жира, содержащегося в х кг продукта Р и в у кг продукта Q, равно 15 х + 4 и по условию диеты не должно превосходить 14:
В свою очередь, количество калорий, содержащихся в х кг продукта Р и в у кг продукта Q, равно 150 х + 200 у и по условию диеты должно быть не меньше 300:
Теперь о стоимости z продуктов. Она равна
и в соответствии с высказанными пожеланиями должна быть минимальной. Последнее записывается так:
Тем самым мы получили систему формул:
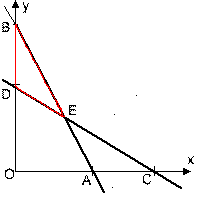
которую решим графическим способом.
Нас интересует только та ее часть, которая лежит над треугольником BDE. Вычисляя значения z во всех трех вершинах этого треугольника
и сравнивая полученные результаты, замечаем, что наименьшее значение (35) достигается в вершине Е. Таким образом,
и искомая пропорция - 2: 3.
|