1. Баскетболист делает три штрафных броска. Вероятность попадания при каждом броске одинакова и равна 0,7. Построить ряд распределения числа попаданий мяча в корзину.
2. Производится  независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события 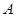 постоянна и равна 0,6. Найти
постоянна и равна 0,6. Найти  случайной величины
случайной величины  - числа появлений события
- числа появлений события 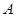 в
в  проведенных испытаниях.
проведенных испытаниях.
3. Случайная величина  распределена равномерно на отрезке [1; 6]. Найти функцию распределения вероятностей
распределена равномерно на отрезке [1; 6]. Найти функцию распределения вероятностей  , математическое ожидание, дисперсию и среднее квадратическое отклонение величины.
, математическое ожидание, дисперсию и среднее квадратическое отклонение величины.
4. Математическое ожидание нормально распределенной случайной величины равно 12, а среднее квалратическое отклонение равно 2. Найти вероятность того, что случайная величина примет значение, заключенное в интервале (14; 16).
5. Случайная величина  распределена по нормальному закону с математическим ожиданием, равным 15, и средним квадратическим отклонением, равным 2. Найти симметричный относительно математического ожидания интервал, в который с вероятностью 0,954 попадет случайная величина.
распределена по нормальному закону с математическим ожиданием, равным 15, и средним квадратическим отклонением, равным 2. Найти симметричный относительно математического ожидания интервал, в который с вероятностью 0,954 попадет случайная величина.

 независимых испытаний, в каждом из которых вероятность появления события
независимых испытаний, в каждом из которых вероятность появления события 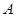 постоянна и равна 0,6. Найти
постоянна и равна 0,6. Найти  случайной величины
случайной величины  - числа появлений события
- числа появлений события  проведенных испытаниях.
проведенных испытаниях. , математическое ожидание, дисперсию и среднее квадратическое отклонение величины.
, математическое ожидание, дисперсию и среднее квадратическое отклонение величины.


