Определение числовых характеристик
Основными числовыми характеристиками распределения случайной величины являются среднее значение, среднее квадратичное отклонение и коэффициент вариации. а) Среднее значение износа
где
Подставляем значения:
б) Среднее квадратическое отклонение: σ = Подставляем:
σ =
в) Коэффициент вариации: V = V = 0,1718 / (0,4564 – 0) = 0,3764. Проверку информации на наличие выпадающих точек осуществляется по формуле: λоп = где Для наименьшего значения износа λоп = (0,195 - 0,045) / 0,1718 = 0,8731. Для наибольшего значения износа
Полученные значения λоп сравниваем с табличными значениями критерия Ирвина. Если λоп >
|
,
– значение износа в середине i -го интервала (середина i -го интервала);
– опытная вероятность в i-ом интервале.
= 0,07 ∙ 0,02 + 0,21 ∙ 0,1 + 0,35 ∙ 0,34 + 0,49 ∙ 0,28 + 0,63 ∙ 0,2 + 0,77 ∙ 0,02 + 0,91 ∙ 0,04 = 0,4564 мм.
0,1718 мм.
,
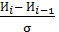и 
– смежные точки в сводной ведомости информации.
= 0,195; 
= 0,045.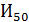
= 0,895; 
= 0,845.
оп = (0,895 - 0,845) / 0,1718 = 0,291.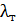
, то такие точки исключают как недостоверные. В нашем случае при α = 0,95 и при N = 50 значение критерия Ирвина λт =1,1 больше λоп. Поэтому с вероятностью 0,95 можно утверждать, что все точки информации достоверны.
