Выбор теоретического закона распреденения износов
Выбор теоретического закона распределения (ТЗР) осуществляется по величине коэффициента вариации V. Если V < 0,3 - то распределение подчиняется закону нормального распределения (ЗНР), если V>0,5 - то распределение подчиняется закону распределения Вейбулла (ЗРВ). В случае, когда V лежит в интервале от 0,3 до 0,5 выбирается тот закон, который лучше совпадает с опытной информацией. Точность совпадения оценивается по критерию согласия. В данном случае коэффициент вариации V = 0,3764. Необходимо рассчитать интегральную F(И) функцию распределения износа детали по ЗНР и ЗРВ, а затем, определив критерий согласия, выбирается ТЗР и рассчитываются его параметры. Значение интегральной функции F( F( где
При этом следует учесть, что Расчёт ведётся для каждого интервала: F1(0,14) = F0[(0,14 - 0,4564)/0,1718] = F0(-1,84) = 1 - F0(1,84) = 1 – 0,97 = 0,03; F2 (0,28) = F0[(0,28 - 0,4564)/ 0,1718] = F0(-1,03) = 1 - F0(1,03) = 1 – 0,85 = 0,15; F3 (0,42) = F0[(0,42 - 0,4564/ 0,1718] = F0(-0,21) = 1 - F0(0,21) = 1 – 0,58 = 0,42; F4 (0,56) = F0[(0,56 - 0,4564)/ 0,1718] = F0(0,6) = 0,73; F5 (0,7) = F0[(0,7 - 0,4564)/ 0,1718] = F0(1,42) = 0,92; F6 (0,84) = F0[(0,84 - 0,4564)/ 0,1718] = F0(2,23) = 0,99; F7 (0,98) = F0[(0,98 - 0,4564)/ 0,1718] = F0(3,05) = 1.
Значение интегральной функции F( по формуле:
где если V = 0,3764, то b = 2,90 и Тогда Расчёт F (0,14) = F (0,28) = F (0,42) = F (0,56) = F (0,7) = F (0,84) = F (0,98) = Для выбора теоретического закона распределения следует определить критерий согласия Колмогорова:
где N – общее количество информации.
Таблица 5. Выбор теоретического закона распределения
Как видно из таблицы 5, для ЗНР Тогда расчетное значение критерия согласия будет равно: для ЗНР для ЗРВ Находим вероятность совпадения теоретических законов с опытным распределением: для ЗНР P( для ЗРВ P( Следовательно, для выравнивания опытной информации ЗНР подходит лучше, чем ЗРВ. Наносим на график (рис.2) значения Определение доверительных границ рассеивания среднего значения износа. Для ЗНР доверительные границы рассеивания среднего значения износа определяют по формулам:
где
Находим:
С вероятностью 0,95 можно утверждать, что среднее значение износа будет находиться в интервале от 0,408 до 0,505 мм.
|

 ) ЗНР в конце i-го интервала определяется по формуле:
) ЗНР в конце i-го интервала определяется по формуле: ,
, – так называемая центрированная интегральная функция. Ее значения табулированы;
– так называемая центрированная интегральная функция. Ее значения табулированы; – среднее значение износа;
– среднее значение износа;
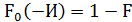 (+И).
(+И). ;
;
 – табулированное значение интегральной функции, принимается в зависимости от
– табулированное значение интегральной функции, принимается в зависимости от  и параметра b;
и параметра b; – сдвиг начала рассеивания;
– сдвиг начала рассеивания; параметр ЗРВ, определяется по формуле
параметр ЗРВ, определяется по формуле  ,
, – коэффициент ЗРВ;
– коэффициент ЗРВ; = 0,51.
= 0,51. для ЗРВ ведётся так же для каждого интервала и полученные данные записываются в статистический ряд.
для ЗРВ ведётся так же для каждого интервала и полученные данные записываются в статистический ряд. (0,14 / 0,51) =
(0,14 / 0,51) =  0,3) = 0,03;
0,3) = 0,03; 0,42/ 0,51) =
0,42/ 0,51) =  0,56 / 0,51) =
0,56 / 0,51) =  (0,7 / 0,51) =
(0,7 / 0,51) =  =
=  ,
, - максимальная абсолютная разность между накопленной опытной вероятностью и теоретической интегральной функцией распределения, то ксть:
- максимальная абсолютная разность между накопленной опытной вероятностью и теоретической интегральной функцией распределения, то ксть: ,
,





 = 0,28;
= 0,28; -
-  ;
;  =
=  и
и  коэффициент Стьюдента, который определяют в зависимости от N и выбранной доверительной вероятности α.
коэффициент Стьюдента, который определяют в зависимости от N и выбранной доверительной вероятности α. = 2,01.
= 2,01.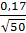 = 0,408 мм;
= 0,408 мм;


