ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ (ч.2)
Они сожгли это на следушей день мальчик написал записку. Вот что там было Контрольная работа. Часть 2 Задача. Путем опроса получены данные (n =80): Выполнить задания: а) получить дискретный вариационный ряд и статистическое распределение выборки; б) построить полигон частот; в) составить ряд распределения относительных частот; г) составить эмпирическую функцию распределения; д) построить график эмпирической функции распределения; е) найти основные числовые характеристики вариационного ряда (по возможности использовать упрощающие формулы для их нахождения): 1) выборочное среднее 2) выборочную дисперсию D (X); 3) выборочное среднее квадратическое отклонение 4) коэффициент вариации V; Вариант 1, Исходные данные
Вариант 2, Исходные данные
Вариант 3, Исходные данные
Вариант 4, Исходные данные
Вариант 5, Исходные данные
Вариант 6, Исходные данные
Вариант 7, Исходные данные
Вариант 8, Исходные данные
ПРИМЕР ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ (ч.2) Задача 2.1. Путем опроса получены следующие данные (n =80):
Выполнить задания: а) получить дискретный вариационный ряд и статистическое распределение выборки; б) построить полигон частот; в) составить ряд распределения относительных частот; г) составить эмпирическую функцию распределения; д) построить график эмпирической функции распределения; е) найти основные числовые характеристики вариационного ряда (по возможности использовать упрощающие формулы для их нахождения): 1) выборочное среднее 2) выборочную дисперсию D (X); 1) выборочное среднее квадратическое отклонение 4) коэффициент вариации V; Решение. а) Для составления дискретного вариационного ряда отсортируем данные опроса по величине и расположим их в порядке возрастания: 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 5 5 5 5 6 6 6 7 7. Статистическое распределение выборки представлено в таблице 6.1, в которой первая строка – варианты (наблюдаемые значение), вторая строка – частоты появления этих вариант). Таблица 6.1. Варианты и их частоты
б) Для построения полигона частот найдем относительные частоты (
Таблица 6.2. Относительные частоты и накопленные частоты
Рис. 6.1. Полигон частот вариационного ряда
в) Запишем ряд распределения (табл. 6.1) относительных частот в виде таблицы 1, в которой первая строка – варианты (изучаемый признак), вторая строка – относительные частоты (частости).
Таблица 6.1. Распределение относительных частот появления признака
г) Эмпирическую функцию распределения найдем, используя накопленные частоты (табл. 6.1, столбик 4) и формулу (4.1):
д) Построим график эмпирической функции распределения (рис. 6.2), используя значения, полученные в пункте г).
Рис. 6.2. График эмпирической функции распределения
е) Для вычисления выборочного среднего
Таблица 6.2. Расчетная таблица для вычисления выборочных величин
Используя суммы, полученные в табл. 6.2, определим искомые величины. 1) Выборочную среднюю 2) Выборочную дисперсию 1) Выборочное среднее квадратическое отклонение
4) Коэффициент вариации Ответ:
|

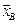 ;
; ;
; , где
, где  , где m – число различных значений признака X (
, где m – число различных значений признака X (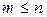 ) и в данном примере m= 8), которые будем вычислять с одинаковой точностью. Полигон частот – ломаная линия, соединяющая точки с координатами
) и в данном примере m= 8), которые будем вычислять с одинаковой точностью. Полигон частот – ломаная линия, соединяющая точки с координатами  (Рис. 6.1). Расчеты запишем в табл. 6.2.
(Рис. 6.1). Расчеты запишем в табл. 6.2.
 Сумма
Сумма

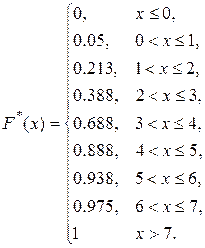

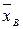 и выборочной дисперсии
и выборочной дисперсии  с использованием приведенных выше формул, удобно составлять расчетную таблицу 6.2:
с использованием приведенных выше формул, удобно составлять расчетную таблицу 6.2:



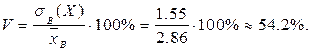
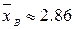 ;
;  ;
; 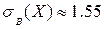 ;
; 



