Модель освоения учебного материала

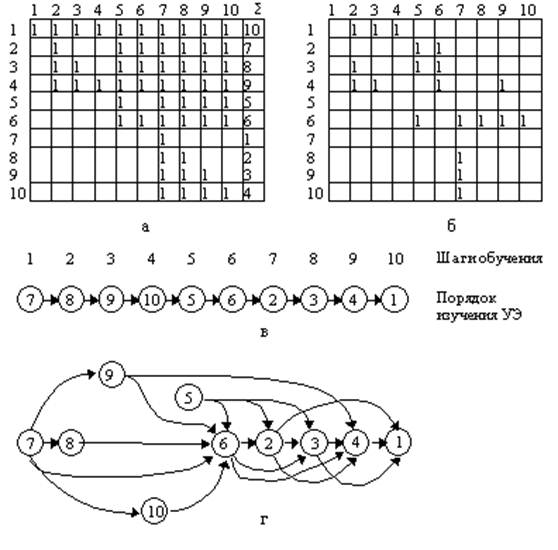
Модель освоения учебного материала показывает, в какой последовательности должны изучаться темы и каковы логические связи между ними.

На начальном этапе проектирования учебного курса планируемый для изучения учебный материал разбивают на отдельные учебные элементы.

В состав модели освоения входят матрицы отношений очередности и логических связей учебных элементов, последовательности изучения учебных элементов, граф логических связей учебных элементов (рис. 3.3.1). Построение модели производят в четыре этапа:

· формирование матрицы отношений очередности учебных элементов;

· обработка матрицы отношений очередности и построение последовательности изучения учебного материала в виде списка учебных элементов;

· формирование матрицы логических связей учебных элементов;

· построение графа логических связей учебных элементов.

 

 

Матрица логических связей — Матрица, показывающая, как учебные элементы связаны друг с другом в пределах курса, раздела и т.д. Матрица является квадратной. Размер равен количеству учебных элементов [ http://www.znannya.org/?view=concept:1017 ]

Матрица отношений очередности — Матрица, показывающая, в какой последовательности должны изучаться учебные элементы [ http://www.znannya.org/?view=concept:1018 ]

 

Матрицы отношений очередности и логических связей учебных элементов являются квадратными. Размер их равен количеству учебных элементов. Сначала строятся пустые матрицы и нумеруются их строки и столбцы в соответствии с возрастанием учебных элементов (см. рис. 3.3.1, а и б). Далее выполняется построчное заполнение ячеек матриц нулями и единицами.

 

Рис. 3.3.1. Пример модели освоения учебного материала:

а - матрица отношений очередности учебных элементов

б - матрица логических связей учебных элементов

в - последовательность изучения учебных элементов

г - граф логических связей

При заполнении ячеек матрицы отношений очередности анализируют отношение очередности между двумя учебными элементами. Единицу ставят в ячейку, если учебный элемент, указанный в номере строки, должен изучаться после учебного элемента, указанного в номере столбца. Противоположное отношение очередности обозначают нулем или оставляют соответствующую ячейку матрицы пустой. Все ячейки главной диагонали матрицы отношений очередности заполняют единицами. Ячейки матрицы, симметричные относительно главной диагонали, должны иметь противоположные значения. Поэтому анализ парных отношений очередности можно проводить лишь для левого нижнего или для правого верхнего треугольника матрицы, заполняя ее оставшуюся часть на основе свойства антисимметрии.

При заполнении матрицы логических связей учебных элементов ставят единицу в ячейку, если учебный материал учебного элемента, указанного в номере строки, логически связан с учебным материалом учебного элемента, указанного в номере столбца. Составление матрицы логических связей удобно вести на основе матрицы отношений очередности путем исключения единиц из тех ячеек, для которых отсутствуют логические, опорные связи между элементами (см. рис. 3.3.1, а и б).

Процесс заполнения матриц целесообразно вести, имея перед глазами тексты с учебным материалом по всем учебным элементам. Анализ содержания учебного материала позволяет более объективно выявлять парные отношения очередности и логические связи между учебными элементами.