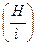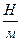Не следует путать понятия чувствительности и точности прибора!
Не следует путать понятия чувствительности и точности прибора! В тех случаях, когда на приборе класс точности не указан, абсолютная погрешность принимается равной половине цены наименьшего деления. Так при измерении линейкой, цена деления которой равна 1мм, допускается абсолютная погрешность 0,5 мм. Точность прибора невозможно превзойти никаким методом измерений на нём. В общем виде при однократном измерении прибором правильный результат выглядит следующим образом. X= Xi ± |∆X |, где X – истинное значение измеряемой величины, Xi - измеренное прибором значение, |∆X | - абсолютная погрешность.
При многократных (серийных) измерениях формула для правильной записи результата выглядит следующим образом: X = X - истинное значение измеряемой величины,
n - измерений можно вычислить по формуле:
Средняя абсолютная погрешность Для оценки точности при многократных измерениях используют понятие относительной погрешности: Ex = Относительная погрешность показывает, какая часть абсолютной погрешности приходится на каждую единицу измеряемой величины, позволяет проводить сравнение точности измерения разнородных физических величин. Например: при измерении бруса длиной l = 1,5 см была допущена абсолютная погрешность 0.03 мм. А при измерении расстояния L = 3,64 ∙ 105 км от Земли до Луны абсолютная погрешность составила 100 км. Может показаться, что первое измерение выполнено намного точнее второго. Однако определены относительные погрешности в первом и во втором случаях: El =
EL =
Очевидно, что второе измерение выполнено в семь раз точнее первого.
Косвенные измерения При косвенных измерениях исследуемая физическая величина является функцией нескольких независимых переменных, которые определяются из прямых измерений. Для определения абсолютных и относительных погрешностей исследуемой величины в этом случае пользуются формулами дифференцирования, т.е. погрешности находят по формулам вычисления дифференциалов функции. Основные правила: а) найти полный дифференциал функции, б) определить абсолютную погрешность, заменив знак дифференциала d на знак абсолютной погрешности ∆ (причём знаки выбираем так, чтобы погрешность получилась максимальной), в) вычислить относительную погрешность измерения искомой величины. Можно пользоваться готовыми формулами, приведёнными в таблице.
Например: поверхностное натяжение определяется по формуле σ = 1) Искомая физическая величина (σ) является функцией двух независимых переменных (F и l), которые определяют посредством прямых измерений. Вычислим полный дифференциал функции: d σ = 2) Заменим знак дифференциала на знак абсолютной погрешности: ∆σ = 3)Вычислим относительную погрешность: Eσ = Выбираем знак так, чтобы погрешность получилась максимальной, т.е. Eσ = В методе отрыва пластинки определяют значения F и l, предположим, что измерения сделаны один раз, l = 3,27см = 3,27 ∙10-2м, m = 250мг = 0,25 ∙10-3 кг, F = mg = 0,25 ∙10-3кг ∙9,8 В соответствии с формулой для расчёта относительной погрешности:
Eσ = Схема отрыва пластинки F измерялась при помощи торсионных весов, шкала которых проградуирована в единицах массы, цена одного деления которой 10-6 кг, поэтому за принимаем половину цены деления шкалы. ∆F =0,5 ∙ 10-6кг ∙9,8
EF =
Длину контура измерим штангенциркулем, цена деления которого 0,2мм, а ∆l = 0,1мм, следовательно: El =
Eσ = 0,2% + 0,3% = 0,5% ∆σ = Eσ ∙σ =(0,5/100) ∙7.49 ∙10-2 ≈ 4 ∙10-4
Окончательный результат: σ = (7.49 ± 0,04) ∙10-2
Нужно отметить, что результат одного измерения не может быть надёжным.
|

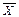 ±
± 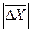 , где
, где - среднее значение измеряемой величины, которое для серии из
- среднее значение измеряемой величины, которое для серии из
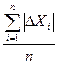 , где
, где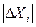 - абсолютные погрешности, вычисленные для каждого из отдельных измерений серии по следующему правилу
- абсолютные погрешности, вычисленные для каждого из отдельных измерений серии по следующему правилу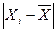 (I = 1,2, …., n)
(I = 1,2, …., n) ∙ 100%
∙ 100%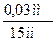 ∙100% = 0,2%
∙100% = 0,2%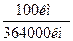 ∙ 100% = 0,03%
∙ 100% = 0,03%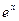
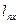 XYZ
XYZ
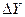 + Y∙
+ Y∙ 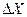 nXn-1 ∙
nXn-1 ∙  YZ∆X + XZ∆Y +XY∆Z
YZ∆X + XZ∆Y +XY∆Z
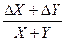
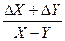
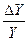 n∙
n∙ 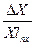

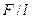 .Определить абсолютную относительность погрешности измерения коэффициента поверхностного натяжения.
.Определить абсолютную относительность погрешности измерения коэффициента поверхностного натяжения.

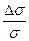 ∙ 100%, Eσ =
∙ 100%, Eσ = 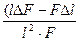 ∙ 100% =
∙ 100% = 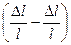 ∙100%
∙100%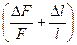 ∙100%
∙100%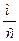 = 245 ∙ 10-5 H, а σ =
= 245 ∙ 10-5 H, а σ = 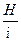
 ∙100% +
∙100% +  ∙100% =EF +El
∙100% =EF +El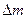
 , а
, а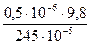 ∙100% = 0,2%
∙100% = 0,2%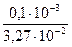 ∙100% = 0,3%
∙100% = 0,3%