Апроксимація
Однією із важливих задач чисельних методів є математичний опис зв'язків в процесах і явищах. Універсальним способом такого опису є аналітична функціональна залежність
якою незалежним змінним Наголосимо, що мова про апроксимацію йде в тому випадку, коли є потреба у визначенні функції Така заміна робиться, якщо нічого невідомо відносно функції Наприклад, у проектуванні мостів, нам завжди потрібна функція, що описує зміну тиску на дану балку прогонової будови в залежності від положення одиничної сили, що переміщається в поперечному напрямку. Сьогодні в теорії споруд немає такої функції в загальному виді. Але її можна одержати апроксимацією дискретного чисельного розв’язку задачі чи на основі таблиці експериментальних даних. Або інший приклад: апроксимація часто потребується там де є підбір аналітичної залежності, що описує результати експерименту. Не менш важливою областю апроксимації є апріорне наближене представлення шуканої функції в чисельних методах теорії споруд.
Як апроксимуючу функцію, часто застосовуються алгебраїчний поліном ступеня n. Така функція має вид:
тобто парабола n – ого ступеня. Полином (1.2) має n+1 коефіцієнт. Відповідним підбором коефіцієнтів можна задовольнити n+1 умов. Підбір виконується шляхом розв’язку системи n+1 лінійних рівнянь з вектором вільних членів з відомих значень функції Звідси випливає, що якщо ми хочемо апроксимувати невідому функцію
При цьому апроксимуюча крива проходить через кожний вузол. Ця загальна процедура припасування кривої і являє собою апроксимацію функції, яка задана таблицею. Проте, в задачі припасування кривої, як правило, не ставиться вимога, щоби крива проходила через кожний вузол. Звичайно криву прагнуть провести так, щоб її відхилення від табличних даних були мінімальними. Найбільш поширеним способом мінімізації відхилення є метод найменших квадратів. За цим методом апроксимуюча функція визначається так, щоб звести до мінімуму суму квадратів різностей між табличними значеннями в вузлах та апроксимуючої кривої. Іншим, дуже поширеним способом апроксимації є застосування сплайнів. Сплайном називається функція виду:
де
У практиці апроксимації найчастіше застосовуються квадратні і кубічні сплайни. Так квадратний сплайн (
Найбільш поширеним, і сьогодні навіть класичним, став кубічний сплайн (n=3). Сплайн третього ступеня має яскраву механічну інтерпретацію: це тонка сталева лінійка, вигнута таким чином, щоб вона стикалася з заданими точками дискретних значень шуканої функції Теорія сплайнової апроксимації інтенсивно розвивалася в останні 30 років і тепер вважається універсальним методом. Апроксимація сплайнами є в усіх відомих математичних і графічних програмних комплексах. В теорії споруд часто застосовується апроксимація тригонометричним поліномом. Функція виду.:
де L – довжина відрізку апроксимації, називається тригонометричним поліномом Наближення тригонометричним поліномом часто застосовується для апроксимації функції в чисельних дискретних розв’язках задач теорії споруд.
|

 , (1.1.)
, (1.1.) ,
,  ставиться у відповідність одне значення функції
ставиться у відповідність одне значення функції 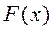 . У кожному конкретному випадку формальне співвідношення (1.1.) має бути представлено певною функцією. Що ж стосується самою функції
. У кожному конкретному випадку формальне співвідношення (1.1.) має бути представлено певною функцією. Що ж стосується самою функції  , як правило, вона невідома. Тоді і залучається апарат чисельних методів, який має назву апроксимація (наближення).
, як правило, вона невідома. Тоді і залучається апарат чисельних методів, який має назву апроксимація (наближення). за допомогою іншої функції
за допомогою іншої функції  або ж є недостатня кількість інформації для її точного визначення.
або ж є недостатня кількість інформації для її точного визначення. , (1.2)
, (1.2) у заданих
у заданих 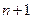 точках (вузлах).
точках (вузлах). так, щоб значення збігалися з
так, щоб значення збігалися з 

 , (1.3)
, (1.3)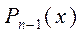 - поліном ступеня не вище
- поліном ступеня не вище  ;
; - коефіцієнти які одержують з умов на кінцях інтервалу апроксимації.
- коефіцієнти які одержують з умов на кінцях інтервалу апроксимації. ) має вигляд:
) має вигляд: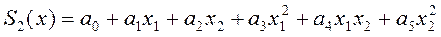 (1.4)
(1.4) . Будучи деформована таким чином, лінійка здобуває форму, при якій запасена в ній пружна енергія мінімальна. Використовуючи теорію вигину бруса при малих деформаціях, можна строго показати, що сплайн – це група сполучених кубічних багаточленів, у місцях сполучення яких перша і друга похідні неперервні.
. Будучи деформована таким чином, лінійка здобуває форму, при якій запасена в ній пружна енергія мінімальна. Використовуючи теорію вигину бруса при малих деформаціях, можна строго показати, що сплайн – це група сполучених кубічних багаточленів, у місцях сполучення яких перша і друга похідні неперервні.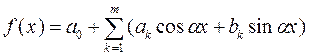 , (1.5)
, (1.5) - параметр поділу інтервалу апроксимації,
- параметр поділу інтервалу апроксимації,  ;
;


