Непрерывные случайные величиныОпределение. Непрерывной называют случайную величину Х, функцию распределения которой F (x) можно представить в виде
Функцию р (х) называют плотностью распределения (вероятностей) случайной величины X. Плотность распределения случайной величины обычно является непрерывной (за исключением, быть может, конечного числа точек) функцией. Следовательно, функция распределения для непрерывной случайной величины является непрерывной на всей числовой оси и в точках непрерывности плотности распределения p (х) имеет место равенство p (x) = F' (x) что следует из свойств интеграла с переменным верхним пределом. Теорема. Плотность распределения обладает следующими свойствами: 1) 2) 3) 4) 5)
|
;
;
;
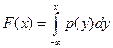
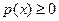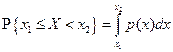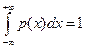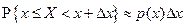в точках непрерывности плотности распределения;
.
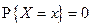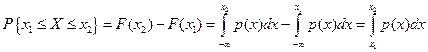3) В частности, при 
, 
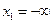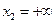событие 
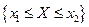является достоверным, и поэтому справедливо утверждение 3.
4) 
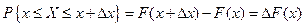. Если 
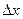мало, то
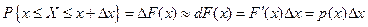5) Поскольку в силу определения функция распределения случайной величины есть несобственный интеграл от плотности, то она является непрерывной, откуда следует утверждение 5.
