Истолкование уравнения БернуллиІ. Гидравлическое истолкование
С точки зрения гидравлики каждый член уравнения имеет свое название
1.
Скоростной напор можно наблюдать в действительности. Если в т. А рядом с пьезометром поставить изогнутую трубку, обращенную отверстием навстречу потоку, то уровень жидкости в этой трубке будет выше уровня в пьезометре на высоту, равную скоростному напору в той точке, гденаходится отверстие трубки
2. Второй член
3. Z1 и Z2 – высоты положения точки живого сечения над плоскостью сравнения.
4. Четвертый член правой части уравнения hw – потери напора при движении жидкости между сечениями 1-1 и 2-2.
Сумма пьезометрической высоты
Сумма скоростного напора
Hd =
Поэтому уравнение Бернулли можно записать в следующем виде:
Hd1 = Hd2 + hw
Т.е. с гидравлической точки зрения уравнение Бернулли может быть прочитано так: гидродинамический напор в данном сечении потока жидкости равен гидродинамическому напору в другом сечении плюс потеря напора между этими сечениями.
ІІ. Геометрическое истолкование уравнения Бернулли В связи с тем, что все члены уравнения Бернулли имеют линейную размерность, его можно представить графически, отложив в каждом сечении от плоскости сравнения О-О по вертикали отрезки, которые равны величинам
Проводя между сечениями 1-1 и 2-2 линию рр (по верхним точкам пьезометрического напора), получим так называемую пьезометрическую линию, которая показывает изменение пьезометрического напора по длине потока. Если расстояние между сечениями по длине потока равно l то можно получить изменение пьезометрического напора на единицу длины потока. Обозначим эту величину Ip. Ip называемую средним пьезометрическим уклоном на данном участке Ip =
Если провести между сечениями 1-1 и 2-2 линию NN (по верхним точкам гидродинамического напора) то получим напорную линию, которая показывает изменение гидродинамического напора по длине потока. Поделив разность гидродинамических напоров в двух сечениях на расстояние между ними, получим средний гидравлический уклон.
i = (Hd1 – Hd2)/ l но Hd1 – Hd2 = hw – потеря напора между сечениями 1-1 и 2-2 поэтому i = hw/ l
Т.е. гидравлическим уклоном называется безразмерная величина, которая показывает изменения гидродинамического напора на единицу длины потока. Т.е. с геометрической точки зрения уравнение Бернулли можно прочитать так: напорная линия по длине потока всегда понижается, так как часть напора тратится на преодоление трения по длине потока.
ІІІ. Энергетическое истолкование уравнения Бернулли Сумму членов уравнения Бернулли с энергетической точки зрения можно представить как сумму удельной кинетической и удельной потенциальной энергий р/γ + Z. В связи с этим можно NN назвать линией полной удельной энергии потока, а линию рр – линией удельной потенциальной энергии. Гидравлический уклон с энергетической точки зрения – это уменьшение полной удельной энергии на единицу длины потока.
П/р Практическое применение уравнения Бернулли
|
- скоростной напор
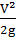. Эта трубка называется гидрометрической или трубкой Пито. Зная разницу уровней в трубке Пито и пьезометре можно определить скорость движения жидкости в этой точке.
и 
называется пьезометрической высотой или приведенной высотой давления пьезометр – если учитывается манометрическое давление приведенной – если учитывается абсолютное давление.
и высоты положения Z во всех точках живого сечения установившегося плавно изменившегося потока одна и та же.
Z = const называется пьезометрическим напором.
и пьезометрического напора.
, 
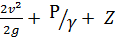
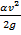- безразмерная величина.
