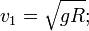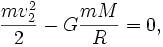Годичным параллаксом звезды p называется угол, под которым со звезды была бы видна большая полуось земной орбиты (равная 1 а. е.), перпендикулярная направлению на звезду.
Расстояние до звезды D, выраженное в тех же единицах, что и длина AO полуоси орбиты Земли задается формулой:
Так как длина AO равна среднему расстоянию от Земли до Солнца (1 а.е.), то в астрономических единицах:
Параллакс звезды всегда ничтожно мал (меньше 1''), поэтому можно использовать формулу для малых углов: Так как Зная соотношение между световым годом и астрономической единицей (1св.год – 63 240 а.е.), можно выразить полученное расстояние в световых годах:
В 1837 г. Впервые были осуществлены надёжные измерения годичного параллакса. Русский астроном Василий Яковлевич Струве (1793-1864) провёл эти измерения для ярчайшей звезды Северного полушария Веги (α Лиры). Почти одновременно в других странах определили параллаксы ещё двух звёзд, одной из которых была α Центавра. Эта звезда, которая с территории России не видна, оказалась ближайшей к нам. Даже у неё годичный параллакс составил всего 0,75''. Под таким углом невооружённому глазу видна проволочка толщиной 1 мм с расстояния 280 м. Поэтому неудивительно, что столь малые угловые смещения так долго не могли заметить. Расстояние до ближайшей звезды., параллакс которой р = 0,75'', составляет
Единицами для измерения столь значительных расстояний являются парсек и световой год. Парсек - это такое расстояние, на котором параллакс равен 1''. Отсюда и название этой единицы: пар – от слова «параллакс», сек – от слова «секунда». Чем меньше параллакс, тем дальше находится звезда. Если, например, p =0.1'', то расстояние до звезды в десять раз больше, чем при p = 1'', т.е. расстояние, выраженное в парсеках, равно обратной величине годичного параллакса, выраженного в секундах дуги. Например, поскольку параллакс α Центавра равен 0,75'', расстояние до неё равно 1,3 парсека. Для выражения очень больших расстояний обычно используют килопарсеки: 1 кпк = 103пк и мегапарсеки: 1 Мпк = 106 пк. Световой год – это такое расстояние, которое свет, распространяясь со скоростью 300 000 км/с, проходит в год. От ближайшей звезды свет идёт до Земли свыше четырёх лет, тогда как от Солнца около восьми минут, а от Луны немногим более одной секунды. К настоящему времени с помощью специального спутника «Гиппаркос» измерены годичные параллаксы более 118 тыс. звёзд с точностью 0,001''. Таким образом, теперь измерением годичного параллакса можно надёжно определить расстояние до звёзд, удалённых от нас на 1000 пк, или 3000 св. лет. Современные телескопы позволяют наблюдать наиболее яркие звёзды даже в других галактиках. Но определить расстояние до далёких звёзд методом тригонометрического параллакса нельзя – слишком малы их параллактические смещения. Расстояния до таких звёзд определяются другими методами. Например, если известна светимость звезды (L) и ее звездная величина (m), расстояние в астрономических единицах вычисляется по формуле:
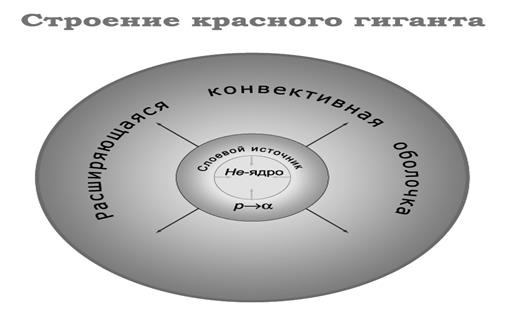
2. По внутреннему строению красные гиганты ничем не отличаются от субгигантов - это звезды, в ядре которых уже закончилось горение водорода. Ядро красных гигантов состоит из вырожденного или нет газа, в зависимости от массы звезды. В звезде продолжаются те же процессы, которые уже обозначились на ветви субгигантов, а именно гелиевое ядро сжимается и нагревается, а оболочка расширяется и охлаждается. На ветви гигантов резко возрастает роль конвекции, до точки 7 (на графиках 1- 2), вырабатываемая энергия передавалась наружу излучением, но температура наружных слоев звезды упала настолько, что большая ее часть становится непрозрачной для излучения и наступает время конвекции. Поверхностная конвективная зона расширяется вниз, до слоев, где шли ядерные реакции и при глубоком перемешивании вещества поверхностный химический состав изменяется, обогащаясь элементами ядерного горения. Иллюстрация такого процесса изображена на врезках (с) графиков 1 и 2. Этот процесс перемешивания конвекцией внешних слоев с внутренними слоями (подвергшимися ядерному преобразованию элементов) из-за расширения вниз конвективной зоны называется "первое вычерпывание" или по-английски "first dredge-up" (точка 8 графиков 1- 2). На ветви гигантов светимость звезды резко возрастает, а поверхностная температура остается почти неизменной. На диаграмме Г-Р звезда резко движется вверх и немного вправо. Во время расширения оболочки ядро продолжает сжиматься и его температура растет. Когда температура ядра достигает примерно 108K, а плотность - 104 (г/см3), гелиевое ядро загорается. Для звезд с массами меньше 3M☉ загорание гелия происходит взрывообразно (так называемая гелиевая вспышка см. Приложение), вырождение газа в ядре снимается и начинается переработка гелий в углерод. Для звезд с массами больше 3M☉ газ в ядре невырожден и процесс загорания гелия происходит спокойно. (см. главу ядерное горение: тройная гелиевая реакция или тройной альфа-процесс). После этого на диаграмме Г-Р звезды уходят с ветви красных гигантов и перемещаются на горизонтальную ветвь. На графике 1 момент гелиевой вспышки это точка 9. На графике 2 спокойное загорание гелия также точка 9 (отметим, что гелий необязательно загорается именно в верхней точке кривой, возможно загорание и раньше, в зависимости от массы и хим. состава звезды). Схематическое изображение красного гиганта показано на рис. 6.
Рис.6. Красный гигант состоит из гелиевого ядра, в котором не происходят ядерные реакции (ядро сжимается), слоевого источника, в котором горит водород, и обширной расширяющейся конвективной оболочки.
Билет КОНФИГУРАЦИЯ - видимое на небе, взаимное расположение тел солнечной системы. Конфигурации нижних (внутренних) планет изображены на первом рисунке. В нижнем и верхнем соединениях планеты в основном не видны, так как, находятся "рядом" с Солнцем. Однако, в нижнем соединении планеты могут проходить по диску Солнца и быть при этом видны. Причем, наблюдения планет в этот момент может дать много информации (атмосфера у Венеры была обнаружена Ломоносовым М. В. именно в этой конфигурации). Периодичность прохождений по диску Солнца такова: Меркурий - май и ноябрь (через 7 и 13 лет(ближайшее прохождение 6.11.2006)), Венера - июнь и декабрь (через 8 и 105,5 лет (ближайшее прохождение 8.06.2004)). Наилучшая видимость внутренних планет достигается в моменты элонгаций (когда планеты максимально удалены от Солнца). При этом планеты видны вечером в восточной элонгации и утром в западной. Конфигурации верхних (внешних) планет изображены на втором рисунке. В общем, верхние планеты наблюдать удобнее нижних, поскольку при своем движении эти планеты не проецируются на небе рядом с Солнцем за исключением момента соединения. Особенно удобным для наблюдения является противостояние. При этом планета ближе всего к Земле, целиком освещена Солнцем, и видна всю ночь. Противостояния Марса происходят приблизительно раз в два года, а раз в 17 лет бывает "великое противостояние", когда Марс максимально приближается к Земле. Марс в этот момент находится в перигелии своей орбиты, а Земля в афелии. 2. К пульсирующим переменным относят те звёзды, переменность которых вызвана процессами, происходящими в их недрах. Эти процессы приводят к периодическому изменению блеска звезды, а вместе с ним и других характеристик звезды — температуры поверхности, радиуса фотосферы и пр. Класс пульсирующих переменных делится на следующие типы: Кривая блеска звезды δ Цефея 1. Долгопериодические цефеиды (Cep) — звёзды высокой светимости с периодами от 1 до ~70 суток. Разделяются на два подтипа: · Классические цефеиды (Cδ) — цефеиды плоской составляющей Галактики · Звёзды типа W Девы (CW) — цефеиды сферической составляющей Галактики 2. Медленные неправильные переменные (L) 3. Звёзды типа Миры Кита (M) 4. Полуправильные переменные (SR) 5. Переменные типа RR Лиры (RR) 6. Переменные типа RV Тельца (RV) 7. Переменные типа β Цефея или типа β Большого Пса (βC) 8. Переменные типа δ Щита (δ Sct) 9. Переменные типа ZZ Кита — пульсирующие белые карлики 10. Магнитные переменные типа α² Гончих Псов (αCV) Теория Пульсирующей Вселенной - ТЕОРИЯ ПУЛЬСИРУЮЩЕЙ ВСЕЛЕННОЙ, вариант теории БОЛЬШОГО ВЗРЫВА, по которомуВселенная проходит последовательные периоды расширения и сжатия. В конце стадии сжатия, когда Вселенная концентрируется в маленьком объеме большой плотности, вероятно, происходит «разлет» Вселенной, называемый взрывом. Таким образом, по этой теорииВселенная бесконечно пульсирует между Большим взрывом и «Большим сжатием». Однако, для того, чтобы так происходило, плотностьВселенной должна была бы быть выше определенного значения (критической плотности), но сжатие Вселенной до таких размеров еще не доказано.
Билет Законы Кеплера были получены им эмпирически в результате исследования видимых движений планет. Поэтому первый закон Кеплера в формулировке, данной в § 40, справедлив лишь в отношении больших планет и тех тел Солнечной системы (некоторых комет, астероидов), которые движутся вокруг Солнца по замкнутым орбитам. Если же иметь в виду движения небесных тел вообще, то на основании предыдущего параграфа этот закон надо сформулировать в следующем виде: под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений — кругу, эллипсу, параболе или гиперболе. В этой формулировке первый закон Кеплера будет справедлив уже для всех комет, орбиты которых либо эллипсы, либо параболы, либо гиперболы; он будет справедлив и для спутников больших планет, орбиты которых эллипсы, но в их фокусах находятся большие планеты, и для физических двойных звезд (см. § 154), обращающихся по эллиптическим орбитам вокруг общего центра масс, и т.д. При этом форма и размеры орбит тел зависят только от величины начальной скорости.
Соотношение (3.12) представляет собой запись третьего обобщенного закона Кеплера. Записав формулу (3.12) для двух тел, массы которых т 1 и т 2, большие полуоси их эллиптических орбит а 1 и a 2, периоды их обращений вокруг центральных тел с массами М 1 и М 2 есть T 1 и T 2, и приняв во внимание, что правые части полученных равенств будут равны, после преобразований получим:
Это есть вторая форма записи третьего обобщенного закона Кеплера. Если рассматривать движение двух планет вокруг Солнца, т.e. вокруг одного и того же тела (М 1= =М 2), и пренебречь массами планет (т 1= m 2 = 0) в сравнении с массой Солнца, то получим формулу (2.7), выведенную Кеплером из наблюдений. Так как массы планет в сравнении с массой Солнца незначительны, то формула Кеплера достаточно хорошо согласуется с наблюдениями. 2. Хотя по человеческой шкале времени звезды и кажутся вечными, они, подобно всему сущему в природе, рождаются, живут и умирают. Согласно общепринятой гипотезе газопылевого облака звезда зарождается в результате гравитационного сжатия межзвездного газопылевого облака. По мере уплотнения такого облака сначала образуется протозвезда, температура в ее центре неуклонно растет, пока не достигает предела, необходимого для того, чтобы скорость теплового движения частиц превысила порог, после которого протоны способны преодолеть макроскопические силы взаимного электростатического отталкивания и вступить в реакцию термоядерного синтеза. В результате многоступенчатых реакций термоядерного синтеза внутренне ядро новорожденной звезды быстро разогревается до сверхвысоких температур, и его избыточная энергия начинает выплескиваться по направлению к ее менее горячей поверхности — и наружу. Одновременно давление в центре звезды начинает расти. Таким образом, «сжигая» водород в процессе термоядерной реакции, звезда не дает силам гравитационного притяжения сжать себя до сверхплотного состояния, противопоставляя гравитационному коллапсу непрерывно возобновляемое внутреннее термическое давление, в результате чего возникает устойчивое энергетическое равновесие. О звездах на стадии активного сжигания водорода говорят, что они находятся на «основной фазе» своего жизненного цикла или эволюции. Рано или поздно, однако, любая звезда израсходует весь пригодный для сжигания в своей термоядерной топке водород. Что дальше? Это также зависит от массы звезды. Солнце (и все звезды, не превышающие его по массе более чем в восемь раз) заканчиваю свою жизнь весьма банальным образом. По мере истощения запасов водорода температура в слоях непосредственно вокруг ядра звезды повышается до уровня, при котором содержащийся там водород вступает, наконец, в реакцию термоядерного синтеза с образованием гелия. В то же время температура в самом ядре, состоящем теперь практически из одного гелия, повышается настолько, что уже сам гелий вступает в новую реакцию термоядерного синтеза: из трех ядер гелия образуется одно ядро углерода. Этот процесс вторичной реакции термоядерного синтеза, топливом для которого служат продукты первичной реакции, — один из ключевых моментов жизненного цикла звезд. Слайд №7 При вторичном сгорании гелия в ядре звезды выделяется так много энергии, что звезда начинает буквально раздуваться. В частности, оболочка Солнца на этой стадии жизни расширится за пределы орбиты Венеры. При этом совокупная энергия излучения звезды остается примерно на том же уровне, что и в течение основной фазы ее жизни, но, поскольку излучается эта энергия теперь через значительно большую площадь поверхности, внешний слой звезды остывает до красной части спектра. Звезда превращается в красный гигант (звёзды с высокой светимостью и протяжёнными оболочками). Для звезд класса Солнца после истощения топлива снова наступает стадия гравитационного коллапса — на этот раз окончательного. Температура внутри ядра больше не способна подняться до уровня, необходимого для начала термоядерной реакции следующего уровня. Поэтому звезда сжимается до тех пор, пока силы гравитационного притяжения не будут уравновешены следующим силовым барьером. Электроны, до этой стадии игравшие роль безработных статистов в эволюции звезды, на определенной стадии сжатия оказываются лишенными «жизненного пространства» и начинают «сопротивляться» дальнейшему гравитационному сжатию звезды. Состояние звезды стабилизируется, и она превращается в вырожденного белого карлика, который будет излучать в пространство остаточное тепло, пока не остынет окончательно. где L• и m• –соответственно светимость и звездная величина Солнца. Билет Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты. Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите. Для вычисления первой космической скорости необходимо рассмотреть равенство центробежной силы и силы тяготения действующих на объект на круговой орбите.
где m — масса объекта, M — масса планеты, G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость, R — радиус планеты. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
Первую космическую скорость можно определить через ускорение свободного падения — так как g = GM/R², то
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела. Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует). Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для Солнца вторая космическая скорость составляет 617,7 км/с. Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе. Вывод формулы: Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния. Запишем закон сохранения энергии
где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G — гравитационная постоянная, v2 — вторая космическая скорость. Разрешая относительно v2, получим
Между первой и второй космическими скоростями существует простое соотношение:
2. Химический состав ядра звезды с помощью спектрального анализа определить невозможно; можно только предполагать, исходя из теоретических расчетов. Химический состав атмосфер звезд и Солнца в основном почти одинаков и близок к химическому составу земной коры, за исключением того, что на Земле нет заметных количеств водорода и гелия (см. таблицу).
В химическом составе некоторых звезд возможны некоторые отклонения от средней нормы. Так, есть звезды, несколько более богатые неоном или стронцием, в некоторых холодных звездах встречается аномально много изотопа углерода 13.
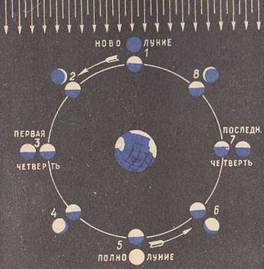
Билет Луна - единственное небесное тело, которое обращается вокруг Земли, если не считать искусственных спутников Земли, созданных человеком за последние годы. Луна непрерывно перемещается по звездному небу и по отношению к какой-нибудь звезде за сутки смещается навстречу суточному вращению неба приблизительно на 13°, а через 27,1/3 суток возвращается к тем же звездам, описав по небесной сфере полный круг. Поэтому промежуток времени, в течение которого Луна совершает полный оборот вокруг Земли по отношению к звездам, называется звездным (или сидерическим) месяцем; он составляет 27,1/3 суток. При своем движении Луна нередко на время загораживает от нас звезды и планеты. Значит, Луна к нам ближе, чем звезды и планеты. Видимое движение Луны по небесной сфере происходит вблизи эклиптики, но плоскость лунной орбиты немного наклонена к ней (на 5°). Точки пересечения лунной орбиты с плоскостью эклиптики называются узлами лунной орбиты. Среднее расстояние Луны от Земли составляет 384 400 км, или приблизительно 30 земных диаметров. Изменение вида Луны - смена ее фаз - происходит от того, что Луна занимает различные положения относительно Земли и освещающего ее Солнца. Луна - это темное шарообразное тело. Когда Луна находится между Землей и Солнцем, обращенное к нам ее полушарие не освещается Солнцем, и мы Луны не видим. Эта фаза Луны называется новолунием. Когда Земля находится между Солнцем и Луной, все обращенное к нам полушарие Луны ярко освещено Солнцем. Эта фаза называется полнолунием. В промежуточных положениях мы видим те или иные части освещенного сбоку полушария Луны: полукруг (первая четверть и последняя четверть), более или менее узкий серп и др. Рисунок 61 показывает связь лунных фаз с положением Луны на ее орбите: солнечные лучи падают сверху, в плоскости чертежа.
Рисунок 61 - Схема, поясняющая смену фаз Луны. Верхняя кульминация Луны происходит при полнолунии - в полночь - около 6ч (по местному времени"). Этим можно пользоваться для приближенной ориентировки на местности или для грубой оценки времени ночью.
|

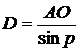

 , где p выражено в радианах.
, где p выражено в радианах. , получаем:
, получаем:  , где p'' – параллакс в секундах дуги.
, где p'' – параллакс в секундах дуги.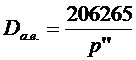


 .
.
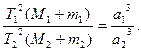
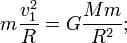
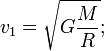
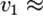 7,9 км/с
7,9 км/с