Динамика контурного фронта
Рассмотрим динамику продвижения к скважине частиц, изначально расположенных на контуре питания Линия изосат – линия, вдоль которой насыщенность принимает постоянное значение. Построим динамику такой линии при разных значениях угла При численных расчетах контур питания, в данном случае, дуга окружности радиуса
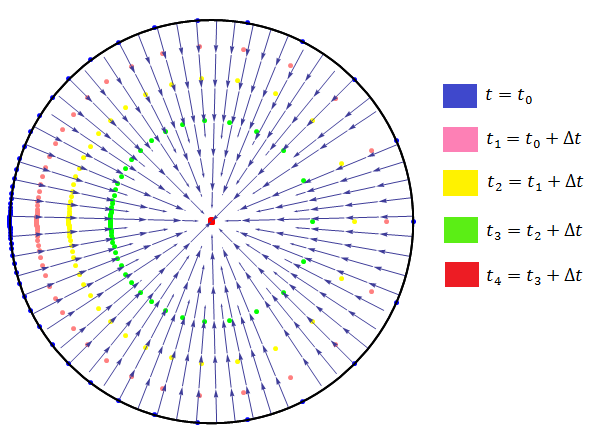
Рис. 16 Положения точек изосат, нанесенные на семейство линий тока при Красным цветом показано расположение точек в такой момент времени, при котором, хотя бы одна точка достигла скважины. Шаг по времени между пересчетом координат точек остальных линий изосат одинаков. На рис.16 видно, что точка, достигшая скважины первой находится по горизонтальной оси. Но при других углах это не выполняется (рис. 17 – 18).
Рис. 17 Положения точек изосат, нанесенные на семейство линий тока при
Рис. 18 Положения точек изосат, нанесенные на семейство линий тока при
Рисунок 19 Положения точек изосат, нанесенные на семейство линий тока при Исследуем теперь зависимость скорости центральной точки от ее расстояния контура питания до скважины. Рассмотрим при разных значениях
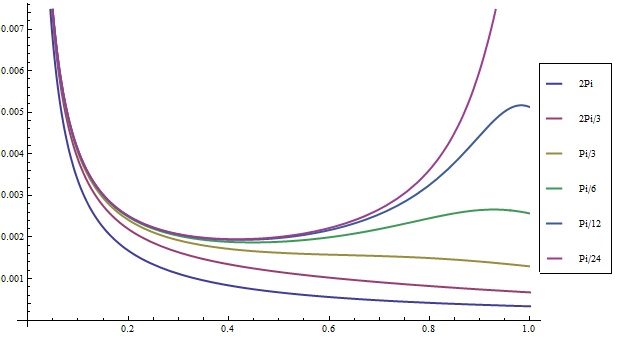
Рис. 20 График зависимости скорости центральной точки от расстояния Для плоскорадиального движения жидкости зависимость скорости движения жидкости от расстояния известна:
Эта зависимость справедлива только для плоскорадиального движения, то есть для угла
|

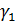 . Данный процесс имеет практический интерес при моделировании притока к скважине некоторой примеси, переносимой насыщающий пласт жидкостью. Кроме того, полученные результаты можно использовать в качестве грубой оценки продвижения к вскрывающей нефтяной пласт скважине фронта воды от контура питания. Упрощение заключается в пренебрежении изменением гидропроводности зоне проникновения воды. В рамках данного упрощения будем далее называть рассматриваемый подвижный фронт изосатой.
. Данный процесс имеет практический интерес при моделировании притока к скважине некоторой примеси, переносимой насыщающий пласт жидкостью. Кроме того, полученные результаты можно использовать в качестве грубой оценки продвижения к вскрывающей нефтяной пласт скважине фронта воды от контура питания. Упрощение заключается в пренебрежении изменением гидропроводности зоне проникновения воды. В рамках данного упрощения будем далее называть рассматриваемый подвижный фронт изосатой.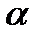 .
. с центральным углом
с центральным углом  , был разделен n точками со сгущением на краях для большей наглядности. Точки изосат были нанесены на семейство линий тока для подробной иллюстрации движения жидкости (рис. 16 – 19).
, был разделен n точками со сгущением на краях для большей наглядности. Точки изосат были нанесены на семейство линий тока для подробной иллюстрации движения жидкости (рис. 16 – 19).





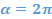
 ,
, – скорость фильтрации,
– скорость фильтрации,  площадь поперечного сечения пласта, нормального к направлению движения жидкости,
площадь поперечного сечения пласта, нормального к направлению движения жидкости, 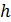 – мощность пласта.
– мощность пласта. . Эту зависимость мы можем наблюдать и на рис. 20. Но с уменьшением угла раствора
. Эту зависимость мы можем наблюдать и на рис. 20. Но с уменьшением угла раствора 


