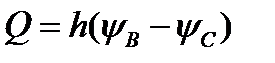Нахождение комплексного потенциала
В силу симметрии задачи относительно оси
Рис. 3 Отображение верхнего полукруга
Рис. 4 Отображение области
Рис. 5 Верхняя полуплоскость Отображение происходит с помощью следующих выражений: 1) 2) 3) 4) В итоге получаем зависимость
Аналогично отображается область
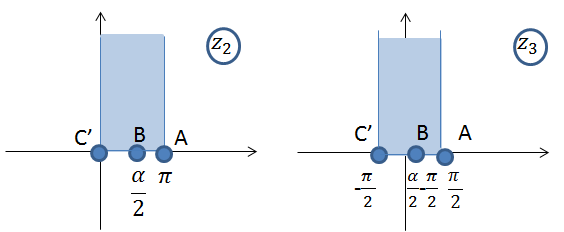
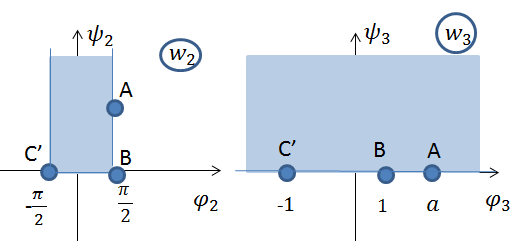
Рис. 6 Отображение области
Рис. 7 Отображение области Отображения последовательно выполняются следующим образом 1) 2) 3)
Окончательно имеем зависимость
Область
Рис. 8 Сопоставление области С помощью формул (1), (2), (3) получаем комплексный потенциал
1.3 Вычисление дебита скважины Рассмотрим комплексный потенциал
Уравнение
где Рассмотрим комплексный потенциал (4) на расстоянии радиуса скважины от начала координат. Выделим реальную часть в комплексном потенциале (4):
В этом выражении величины
Мнимая часть комплексного потенциала
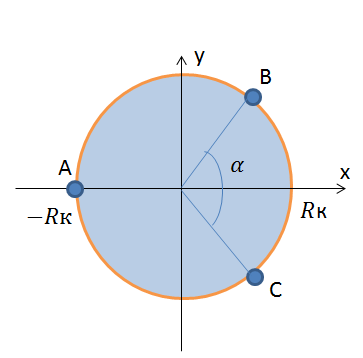
Рис. 9 Схема кругового пласта
|

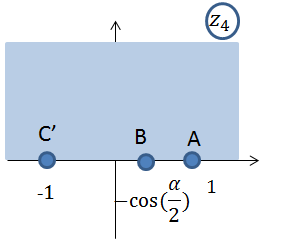
 будет рассматриваться только верхний полукруг. Последовательно отображается область
будет рассматриваться только верхний полукруг. Последовательно отображается область 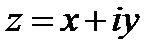 на верхнюю полуплоскость, как показано на рис.3 – 5.
на верхнюю полуплоскость, как показано на рис.3 – 5.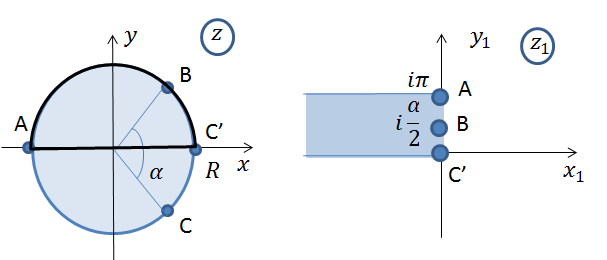
 на полуполосу
на полуполосу 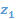
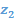 на
на 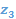

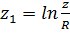 ;
;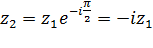 ;
;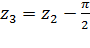 ;
;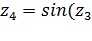 ).
).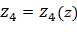 :
: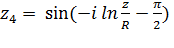 (1)
(1)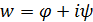 на верхнюю полуплоскость
на верхнюю полуплоскость  (рис. 6 – 7).
(рис. 6 – 7).
 на
на 
 на
на 
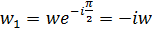
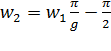
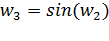
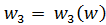 :
: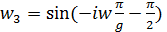 (2)
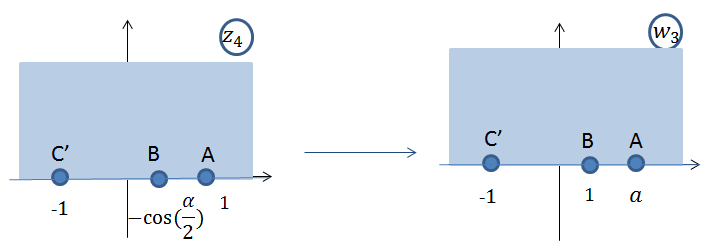
(2) переходит в область
переходит в область 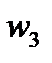 с помощью дробно – линейного преобразования (рис.8).
с помощью дробно – линейного преобразования (рис.8).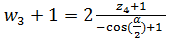 (3)
(3)
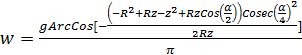 . (4)
. (4)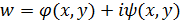 .
.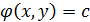 определяет семейство эквипотенциалей, совпадающих с изобарами [2,3]:
определяет семейство эквипотенциалей, совпадающих с изобарами [2,3]: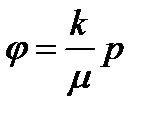 , (5)
, (5)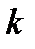 – коэффициент проницаемости пласта,
– коэффициент проницаемости пласта, 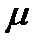 – динамический коэффициент вязкости насыщающей пласт жидкости,
– динамический коэффициент вязкости насыщающей пласт жидкости, 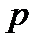 – давление в жидкости.
– давление в жидкости.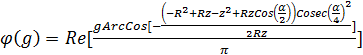 .
.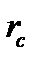 ,
, 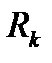 ,
, 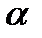 считаются известными, а величина
считаются известными, а величина  неизвестна. Приравнивая между собой правые части (4), (5), можно найти неявную зависимость параметра комплексного отображения
неизвестна. Приравнивая между собой правые части (4), (5), можно найти неявную зависимость параметра комплексного отображения 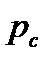 ,
, 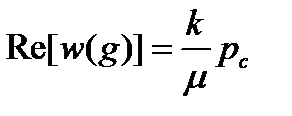 .
.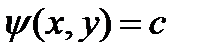 представляет собой семейство линии тока. Дебит
представляет собой семейство линии тока. Дебит 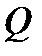 вычисляется как разность крайних значений функции тока, умноженная на мощность пласта
вычисляется как разность крайних значений функции тока, умноженная на мощность пласта 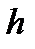 (точки
(точки 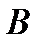 и
и 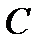 изображены на рис. 9):
изображены на рис. 9):