В задачнике [1] приводится задача со следующими данными:радиус скважины  =10 см; радиус пласта
=10 см; радиус пласта  =350 м; коэффициент проницаемости
=350 м; коэффициент проницаемости  =0.8 Д; динамический коэффициент вязкости
=0.8 Д; динамический коэффициент вязкости  =5 сП; давление на контуре питания
=5 сП; давление на контуре питания  =27.9 МПа; давление на забое скважины
=27.9 МПа; давление на забое скважины 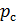 =7.84 МПа; центральный угол
=7.84 МПа; центральный угол  =120
=120 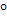 ; мощность пласта
; мощность пласта  =12 м.
=12 м.
Найдем величину  и дебит скважины (вычисления проводились с использованием математического пакета Wolfram Mathematica 8).
и дебит скважины (вычисления проводились с использованием математического пакета Wolfram Mathematica 8).

В данном случае 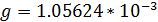 .
.
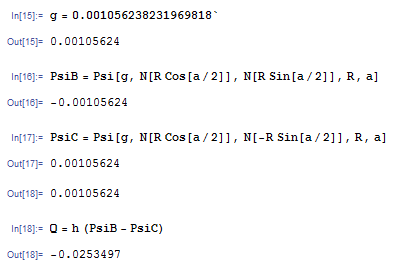
Дебит при вышеперечисленных данных равен 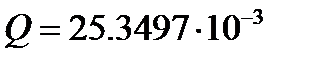
 . Если же решать задачу предложенным в задачнике [1] методом осреднения контурного давления по всей длине окружности пласта и сведением ее к плоскорадиальной, то получим
. Если же решать задачу предложенным в задачнике [1] методом осреднения контурного давления по всей длине окружности пласта и сведением ее к плоскорадиальной, то получим 
 . Ответы значительно отличаются друг от друга. Это означает, что решение, приведенное в задачнике, не применимо к данной задаче.
. Ответы значительно отличаются друг от друга. Это означает, что решение, приведенное в задачнике, не применимо к данной задаче.
3. Исследование дебита при разных углах 
Рассмотрим дебит при различных углах раскрытия проницаемого контура пласта 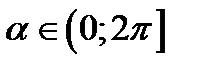 (рис.10), полученный описанным методом с применением теории комплексного потенциала.
(рис.10), полученный описанным методом с применением теории комплексного потенциала.
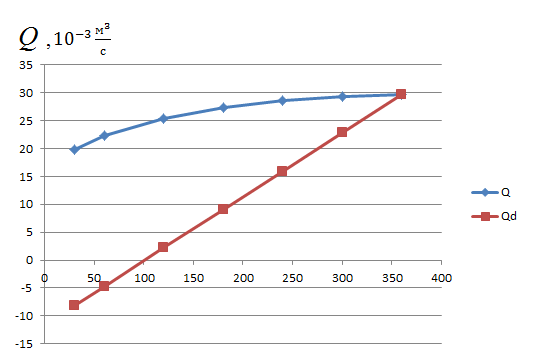
Рис. 10 Зависимость дебита скважины от угла 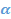
По графику видно, что с увеличением угла раствора  увеличивается и дебит скважины
увеличивается и дебит скважины  , при этом зависимость имеет нелинейный характер, стремясь к дебиту скважины в круговом пласте с полностью проницаемым контуром.
, при этом зависимость имеет нелинейный характер, стремясь к дебиту скважины в круговом пласте с полностью проницаемым контуром.
В случае, когда угол  , движение будет плоскорадиальным. При плоскорадиальном движении векторы скорости фильтрации направлены по радиусам к оси скважины. Если на внешней границе пласта, совпадающей с контуром питания, поддерживается постоянное давление
, движение будет плоскорадиальным. При плоскорадиальном движении векторы скорости фильтрации направлены по радиусам к оси скважины. Если на внешней границе пласта, совпадающей с контуром питания, поддерживается постоянное давление  , а на забое скважины постоянное давление
, а на забое скважины постоянное давление  , пласт однороден по пористости и проницаемости, фильтрация происходит по закону Дарси, то объемный дебит скважины определится по формуле Дюпюи:
, пласт однороден по пористости и проницаемости, фильтрация происходит по закону Дарси, то объемный дебит скважины определится по формуле Дюпюи:
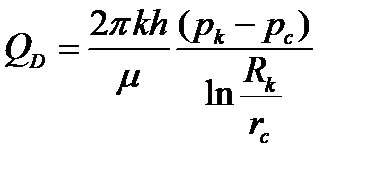
Дебит, рассчитанный по данной формуле, равен 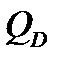 =
=  и в точности совпадает с дебитом, вычисленным с помощью комплексного потенциала.
и в точности совпадает с дебитом, вычисленным с помощью комплексного потенциала.

 =10 см; радиус пласта
=10 см; радиус пласта  =350 м; коэффициент проницаемости
=350 м; коэффициент проницаемости  =0.8 Д; динамический коэффициент вязкости
=0.8 Д; динамический коэффициент вязкости  =5 сП; давление на контуре питания
=5 сП; давление на контуре питания  =27.9 МПа; давление на забое скважины
=27.9 МПа; давление на забое скважины 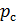 =7.84 МПа; центральный угол
=7.84 МПа; центральный угол  =120
=120 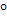 ; мощность пласта
; мощность пласта  =12 м.
=12 м. и дебит скважины (вычисления проводились с использованием математического пакета Wolfram Mathematica 8).
и дебит скважины (вычисления проводились с использованием математического пакета Wolfram Mathematica 8).
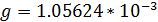 .
.
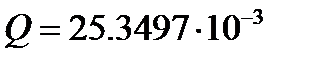
 . Если же решать задачу предложенным в задачнике [1] методом осреднения контурного давления по всей длине окружности пласта и сведением ее к плоскорадиальной, то получим
. Если же решать задачу предложенным в задачнике [1] методом осреднения контурного давления по всей длине окружности пласта и сведением ее к плоскорадиальной, то получим 

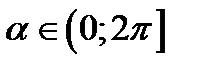 (рис.10), полученный описанным методом с применением теории комплексного потенциала.
(рис.10), полученный описанным методом с применением теории комплексного потенциала.
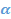
 , при этом зависимость имеет нелинейный характер, стремясь к дебиту скважины в круговом пласте с полностью проницаемым контуром.
, при этом зависимость имеет нелинейный характер, стремясь к дебиту скважины в круговом пласте с полностью проницаемым контуром. , движение будет плоскорадиальным. При плоскорадиальном движении векторы скорости фильтрации направлены по радиусам к оси скважины. Если на внешней границе пласта, совпадающей с контуром питания, поддерживается постоянное давление
, движение будет плоскорадиальным. При плоскорадиальном движении векторы скорости фильтрации направлены по радиусам к оси скважины. Если на внешней границе пласта, совпадающей с контуром питания, поддерживается постоянное давление  , а на забое скважины постоянное давление
, а на забое скважины постоянное давление  , пласт однороден по пористости и проницаемости, фильтрация происходит по закону Дарси, то объемный дебит скважины определится по формуле Дюпюи:
, пласт однороден по пористости и проницаемости, фильтрация происходит по закону Дарси, то объемный дебит скважины определится по формуле Дюпюи: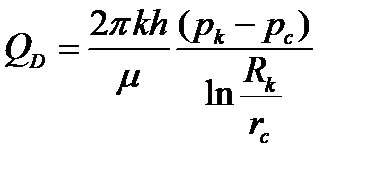
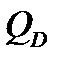 =
=  и в точности совпадает с дебитом, вычисленным с помощью комплексного потенциала.
и в точности совпадает с дебитом, вычисленным с помощью комплексного потенциала. 


