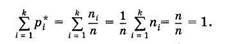Распределение частиц по потенциальным энергиям в силовых полях — гравитационном, электрическом и др. — называют распределением Больцмана.
Применительно к гравитационному полю это распределение может быть записано в виде зависимости концентрации п молекул от высоты h над уровнем Земли или от потенциальной энергии молекулы m0gh:
Выражение (2.40) справедливо для частиц идеального газа. Графически эта экспоненциальная зависимость изображена на рис. 2.8. Такое распределение молекул в поле тяготения Земли можно качественно, в рамках молекулярно-кинетических
объяснить тем, что на молекулы оказывают влияние два противоположных фактора: гравитационное поле, под действием которого все молекулы притягиваются к Земле, и молекулярно-хаотическое движение, стремящееся равномерно разбросать молекулы по всему, возможному объему. В заключение полезно заметить некоторое сходство экспоненциальных членов в распределениях Максвелла и Больцмана:
Г ЛАВА 3 Математическая статистика Методы математической статистики позволяют систематизировать и оценивать экспериментальные данные, которые рассматриваются как случайные величины. Основные понятия математической статистики В главе 2 были рассмотрены некоторые понятия и закономерности, которым подчинены массовые случайные явления. Одной из практических задач, связанных с этим, является создание методов отбора данных (статистические данные) из большой совокупности и их обработки. Такие вопросы рассматриваются в математической статистике. Математическая статистика — наука о математических методах систематизации и использования статистических данных для решения научных и практических задач. Математическая статистика тесно примыкает к теории вероятностей и базируется на ее понятиях. Однако главным в математической статистике является не распределение случайных величин, а анализ статистических данных и выяснение, какому распределению они соответствуют. Предположим, что необходимо изучить множество объектов по какому-либо признаку. Это возможно сделать, либо проведя сплошное наблюдение (исследование, измерение), либо не сплошное, выборочное. Выборочное, т. е. неполное, обследование может оказаться предпочтительнее по следующим причинам. Во-первых, естественно, что обследование части менее трудоемко, чем обследование целого; следовательно, одна из причин — экономическая. Во-вторых, может оказаться и так, что сплошное обследование просто нереально. Для того чтобы его провести, возможно, нужно уничтожить всю исследуемую технику или загубить все исследуемые биологические объекты. Так, например, врач, имплантирующий электроды в улитку для кохлеарного протезирования (см. § 6.5), должен иметь вероятностные представления о расположении улитки слухового аппарата. Казалось бы, наиболее достоверно такие сведения можно было получить при сплошном патологоанатомическом вскрытии всех умерших с производством соответствующих замеров. Однако достаточно собрать нужные сведения при выборочных измерениях. Большая статистическая совокупность, из которой отбирается часть объектов для исследования, называется генеральной совокупностью, а множество объектов, отобранных из нее, — выборочной совокупностью, или выборкой. Свойство объектов выборки должно соответствовать свойству объектов генеральной совокупности, или, как принято говорить, выборка должна быть представительной (репрезентативной). Так, например, если целью является изучение состояния здоровья населения большого города, то нельзя воспользоваться выборкой населения, проживающего в одном из районов города. Условия проживания в разных районах могут отличаться (различная влажность, наличие предприятий, жилищных строений и т. п.) и таким образом, влиять на состояние здоровья. Поэтому выборка должна представлять случайно отобранные объекты. Если записать в последовательности измерений все значения величины х в выборке, то получим простой статистический ряд. Например, рост мужчин (см): 171, 172, 172, 168, 170, 169,.... Такой ряд неудобен для анализа, так как в нем нет последовательности возрастания (или убывания) значений, встречаются и повторяющиеся величины. Поэтому целесообразно ранжировать ряд, например, в возрастающем порядке значений и указать их повторяемость. Тогда статистическое распределение выборки:
Здесь xi — наблюдаемые значения признака (варианта); ni — Число наблюдений варианты xi (частота); рi* — относительная Частота. Общее число объектов в выборке (объем выборки)
всегo k вариант. Статистическое распределение — это совокупность вариант и соответствующих им частот (или относительных растет), т. е. это совокупность данных 1-й и 2-й строки или 1-й и 3-й строки в (3.1). В медицинской литературе статистическое распределение, состоящее из вариант и соответствующих им частот, получило название вариационного ряда. Наряду с дискретным (точечным) статистическим распределением, которое было описано, используют непрерывное (интервальное) статистическое распределение:
Здесь xl _ 1, xi — 1-й интервал, в котором заключено количественное значение признака; ni — сумма частот вариант, попавших в этот интервал; р* — сумма относительных частот. В качестве примера дискретного статистического распределения укажем массы новорожденных мальчиков (кг) и частоты (табл. 5).
Таблица 5
Общее количество мальчиков (объем выборки)
Можно это распределение представить и как непрерывное (интервальное) (табл. 6). Таблица 6
Для наглядности статистические распределения изображают графически в виде полигона и гистограммы. Полигон частот — ломаная линия, отрезки которой соединяют точки с координатами (х1; п1), (х2; п2),... или для полигона относительных частот — с координатами (x1; р*), (х2; р*),... (рис. 3.1). Рис. 3.1 относится к распределению, представленному в табл. 5. Гистограмма частот — совокупность смежных прямоугольников, построенных на одной прямой линии (рис. 3.2), основания
Таким образом, площадь каждого прямоугольника равна соответственно
Следовательно, площадь гистограммы частот и площадь гистограммы относительных частот
Наиболее распространенными характеристиками статистического распределения являются средние величины: мода, медиана и средняя арифметическая, или выборочная средняя. Мода (Мо) равна варианте, которой соответствует наибольшая частота. В распределении массы новорожденных (см. табл. 5) Мо = 3,3кг. Медиана (Me) равна варианте, которая расположена в середине статистического распределения. Она делит статистический (вариационный) ряд на две равные части. При четном числе вариант за медиану принимают среднее значение из двух центральных вариант. В рассмотренном распределении (см. табл. 5) Me = 3,4 кг. Выборочная средняя (хв) определяется как среднее арифметическое значение вариант статистического ряда:
Для примера (см. табл. 5)
Для характеристики рассеяния вариант вокруг своего среднего значения хв вводят характеристику, называемую выборочной дисперсией, — среднее арифметическое квадратов отклонения вариант от их среднего значения:
Квадратный корень из выборочной дисперсии называют выборочный средним квадратическим отклонением:
Для примера (см. табл. 5)
|




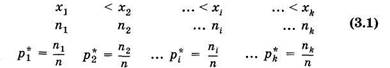



 прямоугольников одинаковы и равны а, а высоты равны отношению частоты (или относительной частоты) к а:
прямоугольников одинаковы и равны а, а высоты равны отношению частоты (или относительной частоты) к а: