Составление композиции законов распределения двух случайных величин
2.1 постановка задачи Дана часть канала передачи информации (измерительного канала), структурная модель которой изображена на рисунке 2.1, где приняты следующие обозначения:
k – коэффициент преобразования линейного звена. Законы распределения и их параметры для СВ Х1 и У, а также значение коэффициента k даны в задании на курсовую работу. Закон распределения СВ Х определяется с учетом линейной связи между СВ Х и Х1 Х=kХ1. СВ Z является суммой двух независимых СВ Z=X+У. Найти композицию законов распределения СВ Х и У, а также определить вероятность попадания СВ Z в заданный интервал.
2.2 исходные данные В таблицу 2.1 заносятся параметры законов распределения и другие данные, необходимые для выполнения второго раздела. Таблица 2.1 Исходные данные
В таблице 2.1 приведены примерные значения параметров варианта 26. СВ Х1 с бесконечными пределами задана математическим ожиданием m и СКО σ. СВ У с конечными пределами задана границами распределения. Коэффициенты q1 и q2 используются для задания границ интервала попадания СВ Z. Коэффициент преобразования линейного звена задан двумя значениями: kс предназначен для группы АС1, kц – для группы АЦ1.
2.3 определение вероятностных характеристик случайных величин Х1, Х, У Дается описание СВ Х1, приводятся ее дифференциальный закон распределения, значения числовых характеристик mх1, Dх1, σ х1 . Если случайная величина задана границами распределения, указываются значения границ и по ним определяются числовые характеристики. Строится график плотности вероятности f (x1). По правилам теории вероятностей определяются числовые характеристики линейной функции Х=kX1: mх= mх1, Dх=k2 Dх1, σ х= Если СВ Х1 является конечной величиной, распределенной в интервале (а1, в1), то СВ Х будет распределена по тому же закону, что и СВ Х1, в интервале с границами а = kа1, в=kв1, где а1, в1, а, в – алгебраические величины. Если одна или обе границы распределения СВ Х1 являются бесконечными, то такие же границы будет иметь СВ Х. После нахождения числовых характеристик СВ Х определяется плотность вероятности f (x) и строится ее график. Заметим, что при умножении СВ Х1 на неслучайный множитель k изменяется конфигурация кривой f (x1), но тип закона распределения остается неизменным. Дается описание СВ У, приводится ее плотность вероятности f (у), значения числовых характеристик my, Dy, σy. Для ограниченной СВ У приводятся границы распределения. Если числовые характеристики СВ У не заданы, то они выражаются через заданные параметры (границы распределения, мода, параметры формы). Строится график кривой f (у).
2.4 составление композиции законов распределения случайных величин х,у Даны две независимые СВ Х и У, известны их плотности вероятности f1 (х) и f2 (у). Требуется найти вероятностные характеристики суммарной СВ Z=Х+У. Числовые характеристики СВ Z определяются по формулам: mz= mх + my; (2.1) Dz= Dх + Dy; (2.2) σz= Если СВ Х и У являются конечными величинами, распределенными в интервалах соответственно (а1, в1) и (а2, в2), то границами СВ Z будут а= а1 + а2, в= в1 + в2, где а1, в1, а2, в2, а, в – алгебраические величины. Если хотя бы одна из СВ Х и У имеет одну или две бесконечных границы, то такие же границы будет иметь и СВ Z. Плотность вероятности g(z), называемая композицией законов f1 (х) и f2 (у), определяется одной из двух формул:
Конкретные выражения g(z) для некоторых сочетаний законов распределения f1 (х) и f2 (у) приведены ниже в п. 2.6.
2.5 определение вероятности попадания случайной величины в заданный интервал К числу практически важных задач относится определение венроятности попадания случайной величины Z в интервал (α, β) Р (α< Z< β) или вероятности ее выхода за границы интервала Р (α> Z> β). В производственных условиях таким интервалом является, например, поле допуска на разброс параметров деталей при механообработке, сопротивлений резисторов и т.д. Рассмотрим два способа определения указанных вероятностей. Первый способ заключается в использовании функции распределения Р (α< Z< β)=G(B)-G(α) или плотности вероятности Р (α< Z< β)= при этом Р (α> Z> β)=1- Р (α< Z< β). Второй способ, по сути, сводится к приближенному определению площади, ограниченной кривой g(z) и осью абсцисс. С этой целью строят кривую g(z) на бумаге, разлинованной в клетку (рисунок 2.2). Пусть общее число клеток в пределах площади под кривой g(z) равно п, площади 1-п1, площади 2- п2, площади 3- п3. Тогда находим: Р (α< Z< β)=
или границы распределения (а,в). Коэффициенты q1, q2 даны в задании на курсовую работу.
2.6 примеры составления композиции законов распределения СВ Х и У
2.6.1 композиция двух нормальных законов СВ Х распределена по нормальному закону с числовыми характеристиками mх, Dх, σх, СВ У – по тому же закону с mу, Dу, σу. По формулам (2.1) – (2.3) определяются числовые характеристики композиции mz, Dz, σz. Плотность вероятности СВ z подчиняется закону:
По формуле (2.5) строится график g(z). Кривая g(z) симметрична относительно точки z=mz, где она имеет максимум g(mz)= Для построения достаточно определить 6-8 точек на одной ветви, например, справа от точки mz в интервале (mz, mz+3 Вероятность попадания СВ z в заданный интервал (α, β) определяется из выражения Р (α< Z< β)= или при α - mz<0 Р (α< Z< β)= Границы интервала находятся по формулам (2.4).
2.6.2 композиция нормального и равномерного законов СВ Х распределена нормально с числовыми характеристиками mх, Dх, σх, СВ У распределена равномерно в интервале (а,в). По значениям а, в подсчитываются mу, Dу, σу, по формулам (2.1) – (2.3) определяются mz, Dz, σz. Плотность вероятности g(z) подчиняется закону:
где c=a+mx, d=в+mx. По формуле (2.6) строится график g(z). Кривая g(z) симметрична относительно точки z=mz, где она имеет максимум g(mz)= Для построения достаточно определить 8-10 точек на правой ветви в интервале (mz, mz+3 Функция распределения СВ z имеет вид:
и используется для нахождения вероятности попадания в заданный интервал Р (α< Z< β)=G(β)- G(α), Р (α> Z> β)=1+G(α)- G(β). Границы интервала (α, β) подсчитываются по формулам (2.4).
2.6.3 композиция равномерного закона и закона релея СВ Х распределена равномерно в интервале с границами а,в, по которым подсчитываются числовые характеристики mх, Dх, σх. СВ У распределена по закону Релея с модой d и плотностью вероятности
Кривая f2(у) обладает положительной ассиметрией, располагается в интервале значений СВ У (0; ∞) и при у=d имеет максимум
Зная моду, находят числовые характеристики закона Релея
По приведенным данным строят графики законов f1(х) и f2(у). Числовые характеристики суммарной случайной величины Z вычисляют по формулам (2.1) – (2.3). Плотность вероятности g(z) описывается двумя формулами
соответствующими двум участкам кривой g(z), состыкованными при z=в. При построении графика функции g(z) учитывают следующие ее особенности: 1) Кривая g(z) имеет положительную ассиметрию и располагается в интервале (а; ∞) значений СВ Z. 2) При z=в ордината g(в) меньше высоты равномерного закона 3) Максимум функции g(z) наблюдается при z >в. 4)в точке z=а касательная к кривой g(z) совпадает с осью абсцисс. Для построения графика g(z) необходимо вычислить не менее 10 точек, из низ 4-5 располагаются на участке, включающем максимум функции g(z). Приведем формулы для вероятности попадания случайной величины в заданные интервалы:
Укажем, что границы интервалов z1 и z2 выражаются через параметры а и в равномерного закона распределения: z1=q1 а; z2=q2 в; коэффициенты q1 и q2 даны в задании на курсовую работу.
2.6.4 композиция двух равномерных законов СВ Х распределена равномерно в интервале (а1,в1) с плотностью вероятности
СВ У распределена по тому же закону в интервале (а2,в2) с плотностью вероятности
По значениям границ интервалов определяются числовые характеристики mх, Dх, σх, mу, Dу, σу, а затем по формулам (2.1) – (2.3) характеристики mz, Dz, σz. Суммарная СВ Z распределена в интервале с границами а3=а1+а2; в3=в1+в2, ее плотность вероятности g(z) имеет вид трапеции, симметричной относительно точки z=mz, и в общем случае состоит из трех участков. Для дальнейших вычислений СВ Х и У рекомендуется привести к центрированной форме:
Соответствующие графики плотности вероятности изображены на рисунках 2.3 и 2.4, где обозначено а=0,5 (в1-а1), в=0,5 (в2-а2).
Приведем выражения для функции распределения
Вероятность попадания случайной величины Р (α< где в качестве G(β) и G(α) берутся те из формул (2.13)-(2.15), для которых в интервалы изменения
2.6.5 композиция равномерного закона и закона симпсона СВ Х распределена равномерно в интервале () с плотностью вероятности
СВ У распределена по закону Симпсона в интервале (а2,в2). плотность вероятности f2(у) имеет вид равнобедренного треугольника с основанием в2-а2 и высотой По значениям границ интервалов подсчитываются числовые характеристики mх=0,5(а1+в1); Dх= mу=0,5(а2+в2); Dу= Числовые характеристики mz, Dz, σz определяются по формулам (2.1)-(2.3). Суммарная СВ z распределена в интервале с границами а3=а1+а2; в3=в1+в2 , ее плотность вероятности g( z ) в общем случае состоит из пяти участков, каждый из которых описывается самостоятельным уравнением. Для упрощения дальнейших вычислений СВ Х и У необходимо приывести к центрированной форме
График Сумма А>в
где Участок 3 описывается прямой линией, остальные участки – параболами, для построения которых берется не менее трех точек, включая границы участков. График функции
2 а<в<2а
Все пять участков кривой
|

 Х1, Х, У, Z – случайные величины (СВ);
Х1, Х, У, Z – случайные величины (СВ); σ х1.
σ х1. . (2.3)
. (2.3)
 .
.
 Р (α> Z> β)=
Р (α> Z> β)=  .
.
 (2.4)
(2.4) . (2.5)
. (2.5) .
. ). Левая ветвь будет зеркальным отображением правой.
). Левая ветвь будет зеркальным отображением правой. ,
, .
. , (2.6)
, (2.6) .
.
 (2.7)
(2.7) , 0≤у<∞.
, 0≤у<∞. .
. ,
, ,
, .
.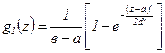 , а≤z≤в; (2.8)
, а≤z≤в; (2.8) , в ≤z<∞, (2.9)
, в ≤z<∞, (2.9) .
.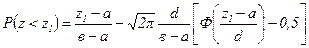 , а≤z1≤в;
, а≤z1≤в; , в ≤z2<∞;
, в ≤z2<∞; .
. .
. .
. .
.


 и
и  является центрированная СВ
является центрированная СВ  , плотность вероятности которой g(
, плотность вероятности которой g(  ) состоит из трех участков (рисунок 2.5) и описывается тремя уравнениями:
) состоит из трех участков (рисунок 2.5) и описывается тремя уравнениями: (2.10)
(2.10) (2.11)
(2.11) (2.12)
(2.12)

 .
. (2.13)
(2.13) (2.14)
(2.14) (2.15)
(2.15) .
. .
. ; σ х=
; σ х=  .
.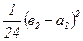 ; σ у=
; σ у=  .
. изображен на рисунке 2.3, где а=0,5 (в1-а1), график
изображен на рисунке 2.3, где а=0,5 (в1-а1), график  представляет собой равнобедренный треугольник с высотой h2 и основанием 2в, где в=0,5 (в2-а2). Треугольник располагается в интервале (-в; в) симметрично относительно точки
представляет собой равнобедренный треугольник с высотой h2 и основанием 2в, где в=0,5 (в2-а2). Треугольник располагается в интервале (-в; в) симметрично относительно точки  =0.
=0. также является центрированной случайной величиной, распределенной в интервале (-а-в, а+в) симметрично относительно точки
также является центрированной случайной величиной, распределенной в интервале (-а-в, а+в) симметрично относительно точки  , уменьшается до трех. Ниже приводятся формулы для
, уменьшается до трех. Ниже приводятся формулы для 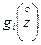 , при этом возможны три случая.
, при этом возможны три случая.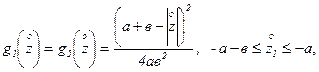 (2.16)
(2.16)
 (2.17)
(2.17)
 (2.18)
(2.18) соответствует участку
соответствует участку  ,
,  ‑ участку
‑ участку  и т.д.
и т.д.
 (2.20)
(2.20)
 (2.21)
(2.21)



