Статистическая обработка опытных данных
Статистическая обработка опытных данных
1.1 исходные данные Исходными данными для первого раздела являются два ряда измерений, являющихся реализациями случайных величин (СВ) Х, У с одинаковыми объемами n. Размер n рекомендуется брать в пределах 50-120. Значения СВ Х, У берутся из выборок, приведенных в [1], §7. пример 1.1 В качестве СВ X берется 76 значений (с 577 по 550) из столбца Z выборки С0, помещенной в [1] на стр. 105. В качестве СВ У берется полностью столбец Z выборки С8 на стр. 117. Значения х1, х2,…, х76 и у1, у2,…, у76 образуют две исходные последовательности и в том же порядке заносятся в таблицу 1.1 Таблица 1.1 Исходные данные
В таблицу 1.2 заносятся упорядоченные значения СВ Х от xmin до xmax и СВ У от уmin до уmax. Значения xi и уi берутся с интервалом, соответствующим точности измерения, в данном случае этот интервал равен единице. В эту же таблицу заносятся абсолютные частоты, т.е. количества значений xi и уi, которые приняли соответственноСВ Х и СВ У. Напротив тех значений xi и уi, которых в действительности нет, проставляются нули или же эти значения не заносятся в таблицу. Таблица 1.2 Первичное распределение
xmin = 437, xmax = 635, размах Rx = 635-437=198; уmin = 23, уmax = 66, размах Rx = 66-23=43. 1.3 составление вторичной таблицы распределения Для компактного представления опытных данных каждую выборку делят на разряды. Число разрядов определяется по формуле:
где k – число разрядов; n – объем выборки. В случае n=76 Затем определяют границы разрядов, при этом рекомендуется выполнить условия: 1) протяженность разряда 2) значения границ разрядов не должны совпадать со значениями случайной величины. Если первое условие не выполняется, то выбирают ближайшее к R значение Здесь возможны следующие варианты. а) xmin –0,5 б) Пусть xmin–0,5; xmin–0,5 или xmin–1,5; xmin–1,5 в) В этом случае сдвиг границ распределения осуществляется внутрь области распределения. Так, при xmin +0,5 а при xmin+0,5; xmin+0,5 или xmin+1,5; xmin+1,5 Необходимо заметить, что значения случайной величины, оказавшиеся при пример 1.2 Для значений СВ х, приведенных в таблице 1.2, имеем: xmin = 437, xmax = 635, Rx = 198,
поэтому изменения размаха Rx не требуется. Чтобы границы разрядов не совпадали со значениями случайной величины, сдвинем область распределения влево на 0,5, тогда получим дробные границы разрядов: 436,5; 458,5; 480,5; …; 634,5. Для значений СВ У имеем: уmin = 23, уmax = 66, Rx =43, Выберем R'у=45, тогда Сдвинем левую границу уmin влево на 1,5, правую границу уmax – вправо на 0,5, тогда границы разрядов примут вид: 21,5; 26,5; 31,5; …; 66,5. Ниже приведена вторичная таблица распределения, в которую наряду с границами разрядов занесены следующие данные: hi и hj – количество элементов в i-м разряде СВ Х и j-м разряде СВ У (абсолютные частоты разрядов);
Таблица 1.3 Вторичное распределение
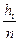 для СВ Х и с hj или для СВ Х и с hj или  для СВ У. для СВ У.
1.4 построение диаграммы рассеивания. Составление корреляционной таблицы Для выявления корреляционной связи между СВ Х и У используют два способа. Первый способ заключается в построении диаграммы рассеивания (или корреляционного поля). С этой целью из таблицы 1.1 берут парные значения и на плоскость х0у наносят n точек с координатами xi и уi. По виду корреляционного поля можно судить о наличии и характере корреляционной связи между случайными величинами.
Второй способ требует определения оценки коэффициента корреляции rxy и проверки гипотезы о его нулевом значении. Для этого составляют корреляционную таблицу, приведенную ниже. Таблица 1.4 Корреляционная таблица
Из таблицы 1.1 берут пары значений xi, уi. Например, первая пара х = 577, у = 44. Значение 577 попадает в седьмой слева разряд Х, значение 44 – в пятый снизу разряд У, поэтому ставится штрих или точка в клетке на пресечении этих разрядов. Вторая пара х = 548, у = 39 дает штрих в клетке на пересечении шестого слева разряда Х и четвертого снизу разряда У. Всего в таблицу заносятся n штрихов, после чего, найдя общее число штрихов в каждой клетке, получают коэффициенты hij и заносят их в соответствующие клетки. Сумма коэффициентов hij в j -й строке дает частоту hj, эти частоты помещают в правом столбце таблицы; сумма коэффициентов hij в i ‑м столбце дает частоту hi, эти частоты помещают в нижней строке таблицы. Значения ui, υj, hi, hj, hij используют для определения статистических характеристик. При выполнении курсовой работы применяют оба способа выявления корреляционной связи между случайными величинами Х и У.
1.5 определение выборочных числовых характеристик Для нахождения коэффициента корреляции необходимо определить следующие выборочные (статистические) числовые характеристики СВ Х и У: выборочные средние
выборочные дисперсии и СКО
ковариацию или выборочный корреляционный момент
Затем находят коэффициент корреляции
пример 1.3 Используя данные таблицы 1.4, подсчитаем статистические числовые характеристики случайных величин Х и У.
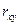 объясняется чисто случайными причинами, главным образом, малым объемом выборок. объясняется чисто случайными причинами, главным образом, малым объемом выборок.
Чтобы убедиться в правильности этого предположения, следует выполнить проверку статистической гипотезы. 1.6 проверка статистической гипотезы. нахождение регрессионной прямой По результатам статистической обработки СВ Х, У определяют коэффициент корреляции, который должен находиться в пределах
В случае Чаще коэффициент корреляции принимает промежуточное значение, и тогда возникает вопрос: связаны ли Х и У корреляционной зависимостью или же событие
Значение Если n-2 находится между двумя табличными значениями, для нахождения размера tα применяют линейную интерполяцию. По результатам сравнения возможны два вывода: 1) 2) Эта зависимость выражается с помощью так называемой регрессионной прямой
коэффициенты которой определяются по правилам теории регрессии [2]
Определив коэффициенты пример 1.4 Для данных примера 1.3 выдвигаем гипотезу Но: rху=0. Зададимся уровнем значимости α=0,01 и найдем число степеней свободы 76-2=74. Определим значение выборочной функции:
Пользуясь таблицей распределения Стьюдента, находим Поскольку z< пример 1.5 Статистическая обработка двух выборок с объемом п=150 дает: mx=7,82; my=7,86; sx=4,86; sy=5,5; sxy=14,2; rxy=0,53. задаемся уровнем значимости α=0,02 и для числа степеней свободы 150-2=148 находим в таблице Стьюдента Подсчитаем коэффициенты регрессионной прямой
1.7 выбор теоретического закона распределения для описания опытных данных На практике часто ставится задача описать полученный опытным путем статистический ряд с помощью подходящего теоретического закона распределения. Обычно такой закон выбирается исходя из физической сущности исследуемого процесса или по внешнему виду эмпирического распределения, например, по виду гистограммы. Решение этой задачи рассмотрим на примере СВ У, статистические характеристики которой приведены в таблицах 1.3 и 1.4. Так как между теоретической кривой и эмпирическим распределением неизбежны расхождения, то возникает вопрос: являются ли эти расхождения случайными вследствие ограниченного числа наблюдений или же подобранная кривая плохо описывает опытные данные. Для ответа на этот вопрос используют критерии согласия, из них наиболее распространенным является критерий В соответствии с критерием Пирсона формируется мера расхождения
где hj – абсолютная частота в j-м разряде; рj – теоретическая вероятность попадания случайной величины в j-й разряд. Распределение r=k-S, где k – число разрядов; S – число связей, наложенных на относительные частоты hj /п. Такими связями могут быть: - условие равенства единице суммы относительных частот, т.е.
- условия равенства важнейших выборочных и теоретических числовых характеристик (моментов), например: а) выборочное среднее должно совпадать с математическим ожиданием m*y=my; (1.4) б) должны совпадать выборочная и теоретическая дисперсии Sy2=Dy=σy2; (1.5) в) должны совпадать третий и четвертый центральные моменты (это условие используется значительно реже). Далее поступают следующим образом. 1) Выдвигается гипотеза о том, что случайная величина У, представленная статистическим рядом, подчиняется некоторому теоретическому закону распределения. 2) Определяется мера расхождения по формуле (1.2). 3) Определяется число степеней свободы r=k-S. 4) По значениям r и В.И. Романовский предложил очень простое правило для применения критерия Пирсона: если ввести обозначение
то при z ≥ 3 гипотеза Н отвергается, а при z <3 эта гипотеза не противоречит опытным данным. пример 1.6 Подобрать теоретический закон распределения для упомянутой выше случайной величины У. 1) Исходя из внешнего вида гистограммы, принадлежащей СВ У, выдвигается гипотеза Н: случайная величина У подчиняется нормальному закону распределения. В качестве числовых характеристик этого закона берутся выборочные числовые характеристики, подсчитанные в п. 1.5: my = m*y=42,68≈42,7; Dy=Sy2=69,58; σy= Sy=8,34. 2) Определяется мера расхождения Для первого разряда
Аналогично
………………………………………………………………
пр8=76 · 0,0503=3,82
пр8=76 · 0,0099=0,75. Результаты вычислений сведены в таблицу 1.5. Как видно из этой таблицы, в первый разряд попадают два значения, а в восьмой и девятый разряды – по одному значению СВ У. Автор книги [2] рекомендует объединять соседние малочисленные разряды, чтобы в каждом разряде было не менее пяти значений. В данном случае следует объединить первый и второй разряды, при этом получается h1;2=2+5=7; np1;2=6,4. Далее объединяем седьмой, восьмой и девятый разряды, при этом h7;8;9=10+1+1=12; np7;8;9=10,91. Суммарное значение Таблица 1.5 Применение критерия Пирсона
r=6-3=3. 4)По значениям r и Правило Романовского дает
Оба результата говорят о том, что гипотеза Н о нормальном распределении СВ У не противоречит опытным данным.
|

 ,
, , т.е.
, т.е.  , и можно принять k=9.
, и можно принять k=9.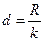 должна выражаться целым числом;
должна выражаться целым числом; , обеспечивающее равенство
, обеспечивающее равенство 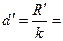 целое.
целое.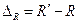 является нечетным положительным числом. Тогда левую границу распределения, например, xmin сдвигают влево по оси x на0,5
является нечетным положительным числом. Тогда левую границу распределения, например, xmin сдвигают влево по оси x на0,5  , правую границу xmax настолько же сдвигают вправо, и границы разрядов принимают вид:
, правую границу xmax настолько же сдвигают вправо, и границы разрядов принимают вид: ; …; xmax +0,5
; …; xmax +0,5 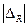 ; xmin +0,5
; xmin +0,5  = целое,
= целое, =дробное.
=дробное. и
и 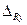 =45-43=2.
=45-43=2. - относительные частоты;
- относительные частоты; и
и  - накопленные частоты или эмпирические вероятности.
- накопленные частоты или эмпирические вероятности.
 ,
, ;
; ,
,  ;
;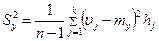 ,
,  ;
; .
. .
.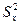 =1958,1;
=1958,1;
 =69,58;
=69,58;
 =4,82;
=4,82;
 =44,25;
=44,25;
 =8,34;
=8,34;


 сравнивают с критическим значением tα, которые берут в таблице распределения Стьюдента [1]. Для входа в таблицу используют два параметра: число степеней свободы n-2 и уровень значимости α (0,005; 0,01; 0,02; 0,05).
сравнивают с критическим значением tα, которые берут в таблице распределения Стьюдента [1]. Для входа в таблицу используют два параметра: число степеней свободы n-2 и уровень значимости α (0,005; 0,01; 0,02; 0,05). , в этом случае считают, что гипотеза Но не противоречит опытным данным, т.е. Х и У не коррелированны.
, в этом случае считают, что гипотеза Но не противоречит опытным данным, т.е. Х и У не коррелированны. , гипотеза Но отклоняется, это означает, что Х и У коррелированны, т.е. СВ У в среднем линейно зависит от СВ Х.
, гипотеза Но отклоняется, это означает, что Х и У коррелированны, т.е. СВ У в среднем линейно зависит от СВ Х. (1.1)
(1.1)
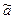 ,
,  , строят прямую (1.1) в той же системе координат, где построена диаграмма рассеивания. Заметим, что в случае принятия гипотезы Но прямая (1.1) не строится.
, строят прямую (1.1) в той же системе координат, где построена диаграмма рассеивания. Заметим, что в случае принятия гипотезы Но прямая (1.1) не строится.
 =2,65.
=2,65. превосходит
превосходит 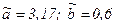 и запишем ее уравнение у=3,17+0,6 х.
и запишем ее уравнение у=3,17+0,6 х. Пирсона.
Пирсона. (1.2)
(1.2) (1.3)
(1.3)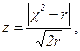
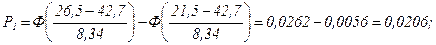 пр1=76 · 0,0206=1,57.
пр1=76 · 0,0206=1,57.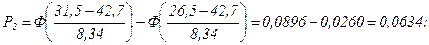 пр2=76 · 0,0636=4,83.
пр2=76 · 0,0636=4,83.
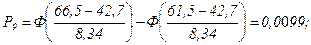
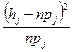
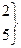 10
18
15
14
10
18
15
14
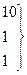
 6,40
10,58
16,24
17,69
13,57
6,40
10,58
16,24
17,69
13,57
 10,91
10,91
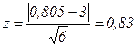 < 3.
< 3.


