Метод геометрической оптики
Для правильного применения методов геометрической оптики и к расчету преобразования оптической системы излучения произвольного типа нужно знать физическое обоснование, на котором базируется геометрическая оптика. Так как излучение имеет электромагнитную природу, то, следовательно, и обоснование должно вытекать из системы уравнений Максвелла или теории дифракции, не ней базирующейся. В пределах гауссовой (параксиальной) оптики линза со светосилой Ф ' может рассматриваться как фазовый транспарант. В курсе "Физическая оптика" было показано, что поле в выходной плоскости ОП3 подобно распределению поля во входной плоскости ОП1, с коэффициентом подобия:
Это выражение позволяет исследовать свойства пучка, преобразованного линзой. 1. Радиус сечения преобразованного пучка r' (z) по уровню амплитуды 1/ е можно найти, если учесть что для сопряженных плоскостей z (a) и z (a') (см. рис. 4) справедливо выражение r' (za') =br (za), где za'=za-a+a' Учитывая соотношение между отрезками (-а), (а) и расстоянием (-а 0) от сечения претяжки до оптической системы
а также выражение (3) для преобразованного пучка может быть получено
2. Поскольку преобразованный пучок гауссов, то для него положение сечения перетяжки [как плоскости с минимальным значением r' (a')] определяется из условия ∂t (a') /∂a' = 0:
Выражения (11) и (12) можно записать в виде
3. Угол расходимости преобразованного пучка можно найти, если учесть, что сечение преобразованного пучка находится в бесконечности, оптически сопряжено с передней фокальной плоскостью линзы:
Из (14) следует, что минимальная расходимость достигается при совпадении сечения перетяжки с фокальной плоскостью линзы. На основании (14) определяется параметр конфокальности преобразованного пучка
4. Использованная методика основана на подобии полей в сопряженных плоскостях и применении методов геометрической оптики. Следовательно, эта методика пригодна для анализа преобразования гауссова пучка и сложной (n -компонентной) оптической системы (см. рис. 5). Характеризуя сложную систему эквивалентной светосилой можно получить выражения для параметров преобразованного пучка, которые аналогичны соответствующим выражениям для одиночной линзы:
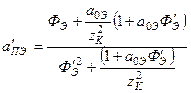
Из (15) следует инвариант преобразования гауссовых пучков
или
Инвариант (16) позволяет сократить число операций при анализе процесса последовательного распространения излучения через ряд оптических систем.
|

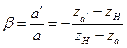 :
: 

 (11)
(11) (12)
(12)

 ;
;  , где
, где 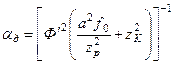 (13)
(13) (14)
(14)


 ;
;  (15)
(15)

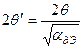

 (16)
(16)



