Интерференционный метод
Действительно, при падении гауссова пучка под углом a на плоскопараллельную пластину толщиной d с показателем преломления n в результате отражения от внешней и внутренней поверхностей пластины формируются два пучка: I 1 и I 2. Оси их параллельны и смещены по координате Ox на величину dx
Кроме того второй пучок приобретает дополнительную разность хода dl. В системе координат (xyz) с осью oz, совпадающей с осью первого отраженного пучка, фазы комплексной амплитуды пучков в точке Q (x,y,z) произвольной плоскости сечения (z) задаются в соответствии с (5) выражениями
Интенсивность светового поля IS (Q) в области интерференции определяется суммарной амплитудой пучков vS (Q) =v 1(Q) +v 2(Q) и описывается выражением
где в соответствии с (17)
Условие D j (Q) = 2pn (n = 0, 1, 2…) определяет точки интерференционной картины с максимальной интенсивностью светового поля. Если измерено расстояние D x = D x (z) между двумя соседними максимумами, т.е. между точками Qn (x,y,z) и Qn +1[ x +D x (z), y, z ], то из уравнения
с учетом (18) следует
откуда
Если измерить D x (z 1) и D x(z 2 = z 1+ z 12), вычислить по (19) радиусы кривизны R (z 1) и R (z 2), а затем записать в соответствии с (3) систему из двух уравнений, то решив эту систему, можно найти конфокальный параметр zK и положение (z 1) сечения перетяжки
затем (по табл.1) вычислить радиус пятна r 0 в сечении перетяжки и расходимость пучка 2 q. Независимость радиуса кривизны волнового фронта от модовых чисел, позволяет использовать этот метод как для одномодовых, так и многомодовых гауссовых пучков. Однако линейная зависимость R (z) от волнового числа (k >>1) и D x / z (см. выражение (19)) приводит вследствие ошибок измерения к существенной абсолютной ошибке вычисления R (z).
|


 (16')
(16')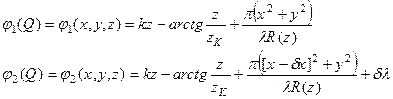 (17)
(17)
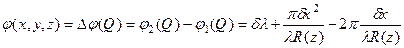 (18)
(18)

 (19)
(19) ;
; 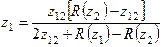 (19')
(19')


