1. Построение графика дробно-линейной функции 
Любую дробно-линейную функцию  можно представить в виде
можно представить в виде  . Таким образом, график ом дробно-линейной функции является гипербола, которую можно получить из гиперболы
. Таким образом, график ом дробно-линейной функции является гипербола, которую можно получить из гиперболы  с помощью двух параллельных переносов - вдоль оси
с помощью двух параллельных переносов - вдоль оси 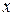 на
на 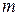 единиц и вдоль оси
единиц и вдоль оси 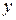 на
на  единиц.
единиц.
Пример. Построить график функции  .
.
Для этого выделим из дроби  целую часть, представив дробь в виде
целую часть, представив дробь в виде  . Имеем:
. Имеем:  .
.
Здесь  ,
,  ,
,  .
.
График функции  можно получить из графика функции
можно получить из графика функции  с помощью двух параллельных переносов: сдвига гиперболы
с помощью двух параллельных переносов: сдвига гиперболы  на 1 единицу вправо вдоль оси
на 1 единицу вправо вдоль оси 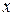 и сдвига полученного графика
и сдвига полученного графика  на 2 единицы вверх в направлении оси
на 2 единицы вверх в направлении оси 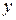 . При этом преобразовании сдвинутся и асимптоты гиперболы
. При этом преобразовании сдвинутся и асимптоты гиперболы  : ось
: ось 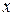 перейдет в прямую
перейдет в прямую  , а ось
, а ось 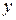 - в прямую
- в прямую  .
.
Для построения графика данной функции проведем в координатной плоскости пунктиром асимптоты: прямую  и прямую
и прямую  . Так как гипербола состоит из двух ветвей, то для построения этих ветвей составим две таблицы: одну для
. Так как гипербола состоит из двух ветвей, то для построения этих ветвей составим две таблицы: одну для  , другую для
, другую для  .
.
| х
| -5
| -3
| -2
| -1
|
|
| х
|
|
|
|
|
|
| у
|
| 0,5
|
| -1
| -4
|
| у
|
|
|
| 3,5
|
|
Отметив в координатной плоскости точки, координаты которых указаны в первой таблице, и соединив их плавной непрерывной линией, получим одну ветвь гиперболы. Аналогично, используя вторую таблицу, получим вторую ветвь гиперболы. График функции  построен (выполните самостоятельно).
построен (выполните самостоятельно).
№ 1. Постройте график функции и найдите асимптоты гиперболы:
Вариант 1.  . Вариант 2.
. Вариант 2.  .
.
2. Построение графика функции 
Функция  (абсолютная величина
(абсолютная величина 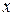 ) задается следующим образом:
) задается следующим образом:
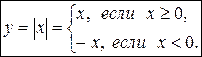
График функции  в промежутке
в промежутке  совпадает с графиком функции
совпадает с графиком функции  , а в промежутке
, а в промежутке  - с графиком функции
- с графиком функции 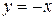 . Он состоит из двух лучей, исходящих из начала координат и являющихся биссектрисами I и II координатных углов.
. Он состоит из двух лучей, исходящих из начала координат и являющихся биссектрисами I и II координатных углов.

Пример. Построить график функции 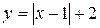 с помощью последовательных преобразований графика функции
с помощью последовательных преобразований графика функции  .
.
Выполним последовательные преобразования графика функции  .
.
График функции  получается из графика функции
получается из графика функции  сдвигом вдоль оси
сдвигом вдоль оси 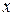 на 1 единицу вправо.
на 1 единицу вправо.
Для получения графика функции  нужно сдвинуть график функции
нужно сдвинуть график функции  на 2 ед. вверх.
на 2 ед. вверх.


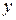

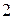
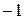


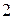
График функции 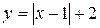
№2. Постройте в одной координатной плоскости графики функций:
Вариант 1. а)  ; б)
; б)  ; в)
; в)  .
.
Вариант 2. а)  ; б)
; б)  ; в)
; в)  .
.
Пример. Построить график функции 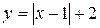 согласно определению абсолютной величины числа.
согласно определению абсолютной величины числа.
Воспользуемся определением абсолютной величины числа.
 ; или
; или  .
.
Тогда  ; или
; или
 .
.
На промежутке  построим прямую
построим прямую 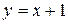 , а на промежутке
, а на промежутке 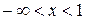 - прямую
- прямую 
 . Для каждой прямой зададим по две точки.
. Для каждой прямой зададим по две точки.

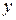

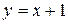
-1 0 1 2 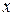
График функции 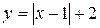
3. Построение графика функции 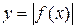
Правило. Чтобы построить график функции  , нужно оставить без изменения те участки графика функции
, нужно оставить без изменения те участки графика функции 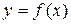 , где
, где  , и зеркально отразить относительно оси
, и зеркально отразить относительно оси 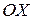 участки графика
участки графика 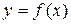 , где
, где  .
.
№3. Построить графики функций, выполняя последовательные преобразования графика 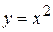 .
.
Вариант 1. а)  ; б)
; б) 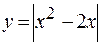 .
.
Вариант 2. а)  ; б)
; б) 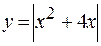 .
.


 . Таким образом, график ом дробно-линейной функции является гипербола, которую можно получить из гиперболы
. Таким образом, график ом дробно-линейной функции является гипербола, которую можно получить из гиперболы  с помощью двух параллельных переносов - вдоль оси
с помощью двух параллельных переносов - вдоль оси 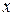 на
на 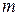 единиц и вдоль оси
единиц и вдоль оси 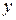 на
на  единиц.
единиц. .
. целую часть, представив дробь в виде
целую часть, представив дробь в виде  . Имеем:
. Имеем:  .
. ,
,  ,
,  .
. можно получить из графика функции
можно получить из графика функции  с помощью двух параллельных переносов: сдвига гиперболы
с помощью двух параллельных переносов: сдвига гиперболы  на 2 единицы вверх в направлении оси
на 2 единицы вверх в направлении оси  , а ось
, а ось  .
. , другую для
, другую для  .
. . Вариант 2.
. Вариант 2.  .
.
 (абсолютная величина
(абсолютная величина 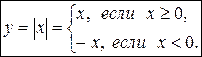
 совпадает с графиком функции
совпадает с графиком функции  , а в промежутке
, а в промежутке  - с графиком функции
- с графиком функции 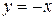 . Он состоит из двух лучей, исходящих из начала координат и являющихся биссектрисами I и II координатных углов.
. Он состоит из двух лучей, исходящих из начала координат и являющихся биссектрисами I и II координатных углов.
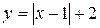 с помощью последовательных преобразований графика функции
с помощью последовательных преобразований графика функции  получается из графика функции
получается из графика функции  нужно сдвинуть график функции
нужно сдвинуть график функции  на 2 ед. вверх.
на 2 ед. вверх.

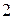
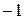


 ; в)
; в)  .
. ; в)
; в)  .
. ; или
; или  .
. ; или
; или .
. построим прямую
построим прямую 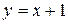 , а на промежутке
, а на промежутке 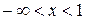 - прямую
- прямую 
 . Для каждой прямой зададим по две точки.
. Для каждой прямой зададим по две точки.
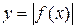
 , нужно оставить без изменения те участки графика функции
, нужно оставить без изменения те участки графика функции 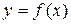 , где
, где  , и зеркально отразить относительно оси
, и зеркально отразить относительно оси  участки графика
участки графика  .
.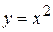 .
. ; б)
; б) 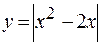 .
. ; б)
; б) 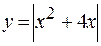 .
.


