Задачи для решения на занятии
Общие правила построения графика функции
§ График функции § График функции § График функции § График функции 1. Построение графика функции № 1. С помощью шаблона графика Вариант 1. а) Вариант 2. а)
2. Построение графика квадратичной функции Способ 1. Для построения графика квадратичной функции запишем формулу Значит, график функции Способ 2. Чтобы построить график функции 1) найти координаты 2) отметить на оси 3) через полученные три точки провести параболу. Если необходимо, можно взять еще пару точек, симметричных относительно оси параболы и построить точки параболы. Соединить точки плавной линией.
№ 2. Построение графика по способу 1. Квадратичная функция задана формулой 1. Запишите формулу 2. Найдите, используя график: · нули функции и промежутки знакопостоянства; · промежутки возрастания и убывания функции, область значений функции. Вариант 1.
№ 3. Построение графика по способу 2. Квадратичная функция задана формулой 1. Найдите координаты вершины параболы. Отметьте на координатной плоскости вершину параболы и проведите ее ось симметрии. Найдите еще две точки на параболе (симметричные относительно оси). Изобразите схематически график. 2. Найдите, используя график: · нули функции и промежутки знакопостоянства; · промежутки возрастания и убывания функции, область значений функции. Вариант 1. 3. Построение графика функции Графиком функции · ветви которой расположены: а) при б) при · асимптотами являются прямые № 4. Дана функция · Постройте график заданной функции. · Найдите область определения функции. · Какие значения принимает функция? · Является ли функция четной или нечетной? · Укажите промежутки возрастания (убывания) функции; промежутки, в которых функция принимает положительные (отрицательные) значения. · Укажите асимптоты гиперболы. · По графику найдите: а) значение Вариант 1. № 5. С помощью шаблона графика Вариант 1. а) Вариант 2. а)
|


 можно получитьиз графика функции
можно получитьиз графика функции  с помощью параллельного переноса вдоль оси
с помощью параллельного переноса вдоль оси 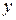 на
на  единиц вверх при
единиц вверх при  , и на
, и на  ед. вниз при
ед. вниз при  .
.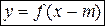 можно получитьиз графика функции
можно получитьиз графика функции 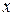 на
на 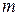 единиц вправо при
единиц вправо при  , и на
, и на  .
.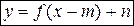 можно получитьиз графика функции
можно получитьиз графика функции  , где
, где 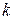 - любое действительное число, можно получитьиз графика функции
- любое действительное число, можно получитьиз графика функции 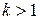 ) и сжатием к оси
) и сжатием к оси  раз (если
раз (если  ).
).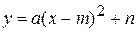
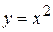 постройтеграфики функций
постройтеграфики функций  , б)
, б)  , в)
, в)  ; г)
; г)  .
.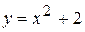 , б)
, б)  , в)
, в)  ; г)
; г)  .
.
 ,
,  .
. с помощью двух параллельных переносов – сдвига вдоль оси
с помощью двух параллельных переносов – сдвига вдоль оси  вершины параболы и отметить ее в координатной плоскости; провести ось параболы – прямую
вершины параболы и отметить ее в координатной плоскости; провести ось параболы – прямую  ;
;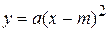 (сдвиг по оси
(сдвиг по оси  . Вариант 2.
. Вариант 2.  .
. . Вариант 2.
. Вариант 2.  .
.
 является гипербола,
является гипербола,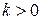 - в I и Ш координатных четвертях,
- в I и Ш координатных четвертях, - во II и IV координатных четвертях;
- во II и IV координатных четвертях; (ось
(ось  (ось
(ось  .
. ; б) значение
; б) значение  .
.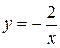 . Вариант 2.
. Вариант 2.  .
. ; б)
; б)  ; в)
; в)  .
. ; б)
; б)  ; в)
; в)  .
.


