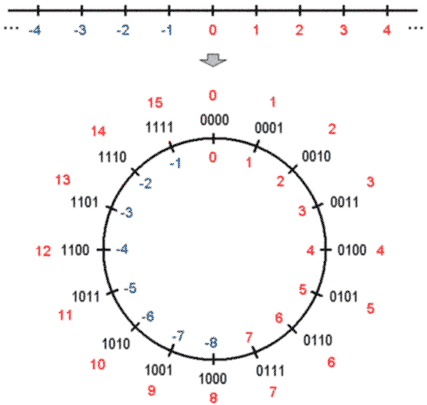
Представление целых чисел со знаком

В обыденной жизни для того, чтобы записать отрицательное число, мы просто ставим перед ним знак "минус". Компьютер же никаких знаков не понимает и умеет работать только с битами, которые могут принимать одно из значений: 0 или 1. При работе с целыми числами всегда используется фиксированное число разрядов (бит). Например, если у нас есть четыре разряда, то мы можем сохранять числа от 0 до 15 (2⁴-1). Это что касается положительных чисел. А как же с отрицательными?

Раз никаких средств поставить "черточку" перед нашими четырьмя битами нет, выделим один из них, например старший, в качестве индикатора знака. Если он равен нулю — число положительное, если единице — отрицательное. Тогда на представление самого числа останутся три бита (а, следовательно, диапазон возможных абсолютных значений сократится вдвое). Есть несколько способов, как использовать эти биты. Первый — записывать в них значение числа по модулю. Вроде бы все просто: число +5 будет выглядеть как 0101, а число -5 — как 1101. Однако такой способ имеет недостатки: во-первых, у нас получаются два представления нуля, +0 (0000) и -0 (1000), а во-вторых, алгоритм сложения и вычитания в микропроцессоре будет сложным и неэффективным.

В большинстве современных процессоров (и, естественно, в MIDI) используется модификация этого способа. Старший бит по-прежнему является показателем знака числа. Положительное число записывается в оставшиеся биты как обычно, а отрицательное занимает все биты в виде так называемого двоичного дополнения своего абсолютного значения. Предположим, нужно записать число -5. Для этого выполняем операцию двоичного дополнения над абсолютным значением (5): инвертируем каждый бит (вместо нуля пишем единицу, и наоборот), а к полученному числу прибавляем 1 (рис. 11). Интересно, что выполнив эту процедуру еще раз, мы получим исходное абсолютное значение.

Наглядное пояснение к такому способу представления дает рис. 12 — числовая прямая при ограниченном диапазоне чисел может быть свернута в круг. На рисунке круг содержит четырехзначные двоичные значения, хотя такое же построение можно провести для любого количества разрядов. Двоичные значения в круге можно рассматривать либо как беззнаковые (тогда их диапазон будет от 0 до 15), либо как числа со знаком (в диапазоне от -8 до +7). В этом состоит одна из главных особенностей представления данных в компьютере: для него любые данные — набор битов, а как их интерпретировать, зависит от программы. Может показаться, что отрицательных чисел здесь на одно больше, чем положительных. Но если ноль принять за положительное число, то все будет "по-честному".

Какие преимущества в таком способе? Во-первых, остается только одно представление нуля. Во-вторых, значительно облегчаются арифметические операции, в частности, довольно сложная (для процессора) операция вычитания может быть выполнена с помощью сложения! Например, для вычитания 3 - 7 компьютер складывает 3 (0011) и двоичное дополнение числа 7 (1001, то есть беззнаковое 9, см. на круге). В результате получается 12 (1100), или -4.

Особенность двоичного дополнения: при разном количестве разрядов одно и то же отрицательное число соответствует разным числам без знака. Так, в предыдущем примере (при разрядности четыре бита) беззнаковому 12 соответствовало -4. Если использовать для хранения числа восемь бит (то есть байт), то -4 будет записано как 11111100, то есть как беззнаковое 252. Есть правило, которое можно использовать для нахождения такого соответствия при любом числе разрядов: нужно сложить отрицательное число с числом 2^N, где N — число разрядов.

В MIDI чаще всего используются 14-битные числа со знаком, то есть в диапазоне от -8192 до +8191. Приведу пример упаковки отрицательного числа в форме двоичного дополнения в MIDI-пару LSB/MSB. Пусть число будет -5833. Складываем его с 16384 (2¹⁴), получаем 10551. Это и будет беззнаковое представление -5833 при разрядности 14 бит. Упакуем его в пару MSB/LSB (подробнее об этом см. вторую статью цикла): MSB = 82 или 0x52 (10551/128), LSB = 55 или 0x37 (10551 — (82 х 128)).