КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ
В стоимость тура включены: · - размещение в номерах с удобствами; · - проезд на автобусе; · - питание по программе; · - экскурсии по программе; · - медицинская страховка; КЛАССИЧЕСКАЯ ТЕОРИЯ ЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ Студентка 3206 группы ИИ Д.Т. Ахунова, научные руководители: канд. тех. наук, доц. кафедры ТиПФ ИИ НГАУ В.Я. Чечуев, доц. кафедры ТиПФ ИИ НГАУ И.М. Дзю
Почти сто лет тому назад П.Друде разработал теорию электро- и теплопроводности металлов, которая была усовершенствована Лоренцем. Применение к этой модели основных положений элементарной молекулярно-кинетической теории привело к поразительным результатам. На основе этих представлений оказалось возможным объяснить законы Видемана-Франца, Ома, Джоуля-Ленца. Для всех перечисленных явлений удалось получить количественные зависимости между величинами, определяющими то или иное явление. В теории Друде валентные электроны металла рассматривались как классический газ (идеальный газ из электронов). Он предположил, что электроны проводимости в металлах ведут себя подобно молекулам идеального газа, и в промежутках между столкновениями движутся совершенно свободно, пробегая в среднем некоторый путь Оценим величину средней скорости
При включении поля на хаотичное тепловое движение со скоростью
где Тогда:
Таким образом, Закон Ома. Друде считал, что при соударении с ионом кристаллической решётки, приобретённая электроном энергия Предположим, что поле, ускоряющее электроны, однородно. Тогда под действием поля электрон получит ускорение
где Друде не учитывал распределение электронов по скоростям и приписывал всем электронам одинаковое значение скорости
Подставим (3) в (2) и получим
Скорость
Подстановка этого выражения в (1) даёт
Мы получили закон Ома в дифференциальной форме:
где проводимость Если бы электроны не сталкивались с ионами решётки, длина свободного пробега Закон Джоуля-Ленца. К концу свободного пробега электрон приобретает дополнительную кинетическую энергию, среднее значение которой равно:
При столкновении с ионом электрон полностью передаёт приобретённую энергию решётке. Эта энергия идёт на увеличение внутренней энергии металла, проявляющейся в его нагревании. Каждый электрон претерпевает за секунду в среднем
где
Соотношение (8) выражает закон Джоуля-Ленца в дифференциальной форме. Закон Видемана-Франца. Из опыта известно, что наряду с высокой электропроводностью металлы отличаются также большой теплопроводностью. Видеман и Франц установили эмпирический закон, по которому отношение коэффициента теплопроводности Из классической теории следует:
Подстановка в (9) числовых значений
которое хорошо согласуется с экспериментальными данными. Однако, когда Лоренц уточнил расчёты, отношение Итак, классическая теория смогла объяснить законы Ома и Джоуля-Ленца, а также дала качественное объяснение закона Видемана — Франца. Вместе с тем эта теория встретилась с весьма существенными недостатками. Такими как: · из формулы (8) вытекает, что сопротивление металлов должно возрастать пропорционально квадратному корню из · чтобы получить закон Ома, пришлось предположить, что электрон при движении сталкивается с узлами кристаллической решётки, а чтобы получить экспериментальное значение удельного сопротивления, приходиться предполагать, что электрон без столкновений может проходить тысячи межузельных расстояний; · теплоёмкость металлов должна быть в 1,5 раза больше теплоёмкости диэлектриков, т.к. электронный газ должен вносить свой вклад в теплоёмкость. В действительности же теплоёмкость металлов не отличается заметно от теплоёмкости диэлектриков. Объяснить эти и другие несоответствия смогла лишь квантовая теория, но там появились уже свои недостатки, т.к. ничего идеального в мире не существует.
|

 . Но, электроны сталкиваются не между собой, а с ионами, образующими кристаллическую решетку. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой.
. Но, электроны сталкиваются не между собой, а с ионами, образующими кристаллическую решетку. Эти столкновения приводят к установлению теплового равновесия между электронным газом и кристаллической решеткой. электронов при
электронов при  :
: м/с.
м/с. . Эту скорость можно выразить их формулы:
. Эту скорость можно выразить их формулы: , (1)
, (1)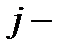 плотность тока, для медных проводов
плотность тока, для медных проводов  .
. м/с.
м/с. . Поэтому при вычислениях модуль результирующей скорости
. Поэтому при вычислениях модуль результирующей скорости  можно заменять модулем теплового движения
можно заменять модулем теплового движения  .
. передаётся иону, а значит, скорость
передаётся иону, а значит, скорость  делается равной нулю.
делается равной нулю. , и к концу пробега скорость упорядоченного движения достигнет в среднем значения
, и к концу пробега скорость упорядоченного движения достигнет в среднем значения , (2)
, (2) среднее время между двумя последовательными соударениями электрона с ионами решётки.
среднее время между двумя последовательными соударениями электрона с ионами решётки. . В этом приближении
. В этом приближении . (3)
. (3) .
.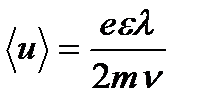 . (4)
. (4) . (5)
. (5)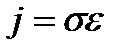 , (6)
, (6) .
.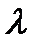 , а следовательно, и проводимость были бы бесконечно велики. Таким образом, согласно классическим представлениям электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами кристаллическими решётки.
, а следовательно, и проводимость были бы бесконечно велики. Таким образом, согласно классическим представлениям электрическое сопротивление металлов обусловлено соударениями свободных электронов с ионами кристаллическими решётки. . (7)
. (7)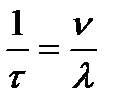 соударений, сообщая всякий раз решётке энергию (7). Поэтому в единице объёма за единицу времени должно выделяться тепло:
соударений, сообщая всякий раз решётке энергию (7). Поэтому в единице объёма за единицу времени должно выделяться тепло: , (8)
, (8) число электронов проводимости в единице объёма;
число электронов проводимости в единице объёма; удельное сопротивление;
удельное сопротивление; удельная тепловая мощность тока.
удельная тепловая мощность тока. к коэффициенту электропроводности
к коэффициенту электропроводности  для всех металлов приблизительно одинаково и изменяется пропорционально температуре.
для всех металлов приблизительно одинаково и изменяется пропорционально температуре. . (9)
. (9) и
и  даёт выражение:
даёт выражение: ,
,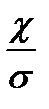 стало хуже сходиться с экспериментом.
стало хуже сходиться с экспериментом.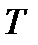 . Скорость же теплового движения пропорциональна корню из
. Скорость же теплового движения пропорциональна корню из 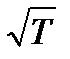 ;
;


