Подбор сечений
Для изготовления сборной панели принимаем бетон класса С Найдем высоту сечения:
leff = lmov–b/2 = 4400–260/2 = 4270мм.=4,27м. Принимаем h = 220мм. Панель рассчитываем как балку двутаврового сечения с заданными размерами bxh = 150x22см(где b – номинальная ширина; h - высота панели). Проектируем панель шестипустотной. Заменяем площадь круглых пустот прямоугольниками той же площади и того же момента инерции. Толщина защитного слоя равна 25мм, так как исходя из СНБ 5.03.01-02 и условий эксплуатации ХC3. Вычисляем: Определяем диаметр пустоты: d= Расстояние между гранью плиты и первой пустотой 85 мм. Проектируем панель семи пустотной. В расчете поперечное сечение пустотной панели приводим к эквивалентному двутавровому сечению. Заменяем площадь круглых пустот прямоугольниками той же площади и того же момента инерции. Вычисляем: Определяем толщину стойки двутавра исходя из того, что сторона квадрата 0,9d = =0,9 Толщина стойки равна: 1500-7
Приведенная толщина панели равна площади полученного двутавра деленной на ширину панели Принимаем hred=15,6см
Рисунок 3.2.1 – Сечение плиты.
Принимаем 7 пустот диаметром 130мм, расстояние между пустотами 70мм. На 1м длины панели шириной действуют следующие нагрузки, кН/м: кратковременная нормативная- кратковременная расчетная - постоянная и длительная расчетная- постоянная и длительная нормативная- итого нормативная- qn + pn = 3+12 = 15 к Н/м; итого расчетная - р + q = 4,5 + 14,938 = 19,438кН/м. Расчетный изгибающий момент от полной нагрузки:
Расчетный изгибающий момент от полной нормативной нагрузки:
то же, от нормативной постоянной и длительной нагрузок:
то же, от нормативной кратковременной нагрузки:
Максимальная поперечная сила на опоре от расчетной нагрузки:
то же от нормативной нагрузки:
|

 ,
,  fc,cube=30MПа,fcm=33MПа,fctm=2,6MПa, fcd=fck/
fc,cube=30MПа,fcm=33MПа,fctm=2,6MПa, fcd=fck/ 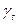 =25/1,5=16,667МПа; продольную арматуру – из стали класса S400, fyd = 367 МПа, fyk=400МПа, армирование отдельными стержнями и каркасами.
=25/1,5=16,667МПа; продольную арматуру – из стали класса S400, fyd = 367 МПа, fyk=400МПа, армирование отдельными стержнями и каркасами.
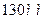
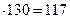 .мм
.мм мм.
мм.
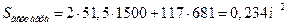


 к Н/м;
к Н/м;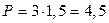 кН/м;
кН/м; кН/м;
кН/м;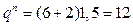 кН/м;
кН/м; к Нм
к Нм кНм
кНм к Нм
к Нм к Нм
к Нм к Н
к Н к Н
к Н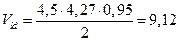 к Н
к Н к Н
к Н


