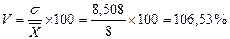Задание 4. С целью изучения затрат времени на обслуживание одного покупателя в магазине бытовой техники было проведено выборочное наблюдение
С целью изучения затрат времени на обслуживание одного покупателя в магазине бытовой техники было проведено выборочное наблюдение. Результат наблюдения представлен в таблице
1. В данном случае необходимо вычислить среднюю интервального ряда. Поэтому в качестве значения признаков в группах принимаются середины интервалов (простая средняя между верхней и нижней границей каждого интервала), в результате чего образуется дискретный ряд.
Данные для расчета среднего времени обслуживания клиентов представлены в таблице.
Тогда время обслуживания клиента составит:
Мода составит (модальный интервал – от 9 до 11 – максимальная частота 24):
Таким образом, 9,13 минут чаще всего тратят продавцы на обслуживание клиента. В данном случае медианный интервал от 7 до 9, т.к. для этого интервала сумма накопленных частот составляет 49, а половина суммы частот ряда составляет 83 / 2 = 41,5. Тогда медиана составляет:
Таким образом, половина продавцов тратит на обслуживание клиентов меньше 8,348 минут, а вторая половина больше. Вспомогательный расчет для определения показателей представлен в таблице.
хср=8 Общая дисперсия составит: Среднее квадратическое отклонение: Отклонение индивидуальных значений от среднего составляет 8,508 минут. Размах вариации: Среднее линейное отклонение:
Относительное линейное отклонение:
Коэффициент вариации составит:
Вывод:среднее время продолжительности разговора 8,145 минуты. 9,13 минут чаще всего уходит на разговоры. Половина разговоров меньше 8,348 минут, а вторая больше. Отклонение индивидуальных значений от среднего составляет 8,508 минут. Т.к. V превышает 40%, то средняя продолжительность разговоров рассчитана по однородной совокупности и является типичной для данной совокупности.
|

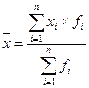 ,
, минут
минут минут.
минут.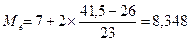 минут.
минут.

 = 12 - 4 = 8 минут.
= 12 - 4 = 8 минут.
 минут
минут .
.